Video: Wat is die integrasie van 1?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Die definitiewe integraal van 1 is die oppervlakte van 'n reghoek tussen x_lo en x_hi waar x_hi > x_lo. In die algemeen, die onbepaalde integraal van 1 is nie gedefinieer nie, behalwe vir 'n onsekerheid van 'n additiewe reële konstante, C. Maar in die spesiale geval wanneer x_lo = 0, die onbepaalde integraal van 1 is gelyk aan x_hi.
Verder, wat is die integraal van 1 u 2?
Deur die magsreël, die integrale van u − 2 met betrekking tot u is - u − 1 . Herskryf − u − 1 +C - u - 1 + C as − 1u +C - 1 u + C.
Behalwe hierbo, wat is die integrasie van 0? Die neem van die afgeleide van enige konstante funksie is 0 , d.w.s. d(c)/dx= 0 Dus die onbepaalde integrale ∫0dx produseer die klas van konstante funksies, dit is f(x)=c vir sommige c. Daar moet ook op gelet word dat die definitiewe integraal van 0 oor enige interval is 0 , as ∫0dx=c−c= 0.
As u dit in die oog hou, wat is die integrasie van enige konstante?
Die integrale van 'n konstant is gelyk daaraan konstant keer die veranderlike van integrasie plus an arbitrêr konstant . Dit is omdat integrasie is die teenoorgestelde van differensiasie.
Hoe integreer jy Cos 2x?
Die integrale van cos ( 2x ) is (1/2)sonde( 2x ) + C, waar C 'n konstante is.
Aanbeveel:
Wat is integrasie in wiskunde met voorbeeld?
Byvoorbeeld, as f = x, en Dg = cos x, dan is ∫x·cos x = x·sin x − ∫sin x = x·sin x − cos x + C. Integrale word gebruik om sulke hoeveelhede soos oppervlakte, volume, werk en, in die algemeen, enige hoeveelheid wat geïnterpreteer kan word as die oppervlakte onder 'n kromme te evalueer
Wat is basiese integrasie?
Basiese integrasieformules. Die fundamentele gebruik van integrasie is as 'n deurlopende weergawe van opsomming. Maar, paradoksaal genoeg, word integrale dikwels bereken deur integrasie te beskou as in wese 'n omgekeerde bewerking tot differensiasie. (Daardie feit is die sogenaamde Fundamentele Stelling van Calculus.)
Wat is die naam van die ensiem wat die sintese van die mRNA-streng kataliseer?
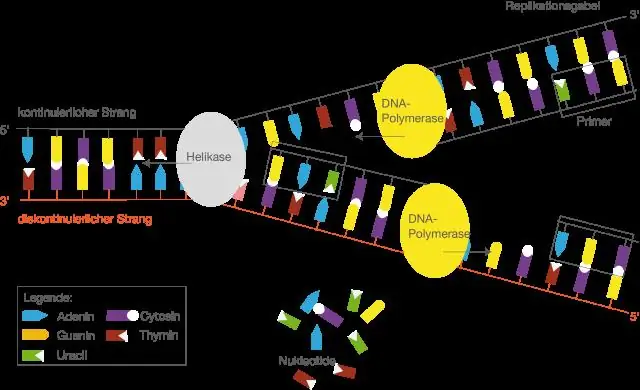
MRNA is "boodskapper" RNA. mRNA word in die kern gesintetiseer deur die nukleotiedvolgorde van DNA as 'n sjabloon te gebruik. Hierdie proses vereis nukleotiedtrifosfate as substrate en word deur die ensiem RNA-polimerase II gekataliseer. Die proses om mRNA van DNA te maak, word transkripsie genoem, en dit vind in die kern plaas
Wat is die reëls van integrasie?
Integrasie Algemene Funksies Funksie Integraal Power Reël (n≠-1) ∫xn dx xn+1n+1 + C Som Reël ∫(f + g) dx ∫f dx + ∫g dx Verskilreël ∫(f - g) dx ∫f dx - ∫g dx Integrasie deur Onderdele Sien Integrasie deur Onderdele
Wat is integrasie in H KMR?
Integrasie is die meting van piekareas op die KMR-spektrum. Dit stem ooreen met die hoeveelheid energie wat geabsorbeer of vrygestel word deur alle kerne wat deelneem aan chemiese verskuiwing tydens die kernspin-flip-proses. Dit word gebruik om die verhouding van waterstof wat met die sein ooreenstem, te bepaal