Video: Wat is identiteitswet in diskrete wiskunde?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Sodat die identiteitswet , p∧T≡p, beteken dat die voegwoord van enige sin p met 'n arbitrêre tautologie T altyd dieselfde waarheidswaarde as p sal hê (d.w.s. sal logies ekwivalent met p wees). Dit beteken dat die disjunksie van enige sin p met 'n arbitrêre tautologie T altyd waar sal wees (sal self 'n tautologie wees).
Om ook te weet is, wat is die identiteitswet in wiskunde?
An identiteit is 'n gelykheid wat geld ongeag die waardes wat vir sy veranderlikes gekies is. Byvoorbeeld, die identiteit (x + y) 2 = x 2 + 2 xy + y 2 (x+y)^2 = x^2 + 2xy + y^2 (x+y)2=x2+2xy+y2 is waar vir alle keuses van x en y, of dit reële of komplekse getalle is.
Verder, wat is 'n voorbeeld van beginsel van identiteit? In logika, die wet van identiteit verklaar dat elke ding identies is met homself. Dit is die eerste van die drie wette van denke, saam met die wet van nie-teenstrydigheid, en die wet van uitgeslote middel. Dit kan ook minder formeel geskryf word aangesien A A is. Een stelling van so 'n beginsel is "Roos is 'n roos is 'n roos is 'n roos."
Vervolgens kan 'n mens ook vra, wat is De Morgan-wet in diskrete wiskunde?
De Morgan se Wette beskryf hoe wiskundig stellings en konsepte word verwant deur hul teenoorgesteldes. In versamelingsteorie, De Morgan se Wette verbind die kruising en vereniging van versamelings deur middel van komplemente. In proposisionele logika, De Morgan se Wette verbind voegwoorde en disjunksies van proposisies deur ontkenning.
Wat is diskrete wiskundige implikasies?
Definisie: Laat p en q proposisies wees. Die stelling "p of q" wat deur p ∨ q aangedui word, is onwaar wanneer beide p en q onwaar is en andersins waar. Die stelling "p impliseer q" wat deur p → q aangedui word, word genoem implikasie . Dit is onwaar wanneer p waar is en q onwaar is en andersins waar is.
Aanbeveel:
Wat is die betekenis van diskrete struktuur?
Diskrete struktuur 'n Stel diskrete elemente waarop sekere bewerkings gedefinieer word. Diskrete impliseer nie-kontinue en daarom sluit diskretesets eindige en telbare versamelings in, maar nie ontelbare versamelings soos die reële getalle
Wat is matrikse in diskrete wiskunde?
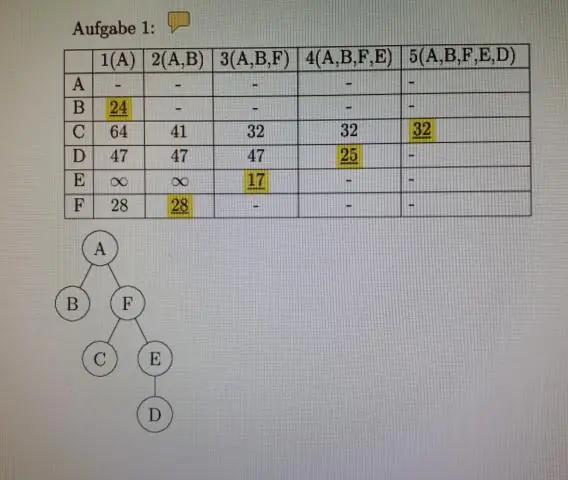
Diskrete Wiskunde en die toepassings daarvan Hoofstuk 2 Aantekeninge 2.6 Matrikse Lesingskyfies Deur Adil Aslammailto:[email protected]. Definisie van matriks •'n Matriks is 'n reghoekige reeks getalle. 'n Matriks met m rye en n kolomme word 'n m x n matriks genoem. Die meervoud van matriks is matrikse
Wat is ekwivalensie in diskrete wiskunde?
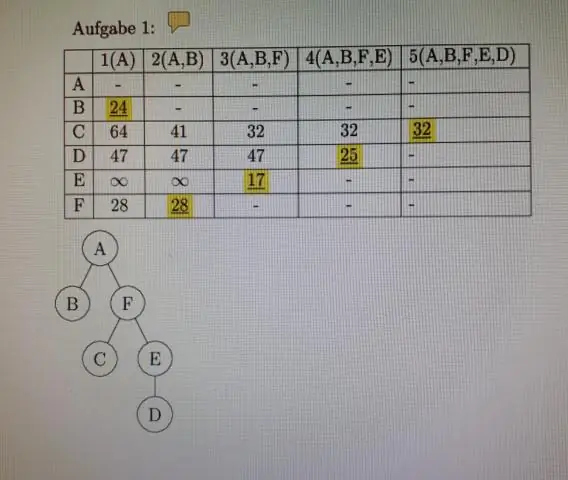
In wiskunde is 'n ekwivalensieverhouding 'n binêre verhouding wat refleksief, simmetries en transitief is. Die relasie 'is gelyk aan' is die kanonieke voorbeeld van 'n ekwivalensieverhouding, waar vir enige voorwerpe a, b en c: a = a (refleksiewe eienskap), as a = b en b = c dan a = c (transitiewe eienskap) )
Wat is stel diskrete wiskunde?
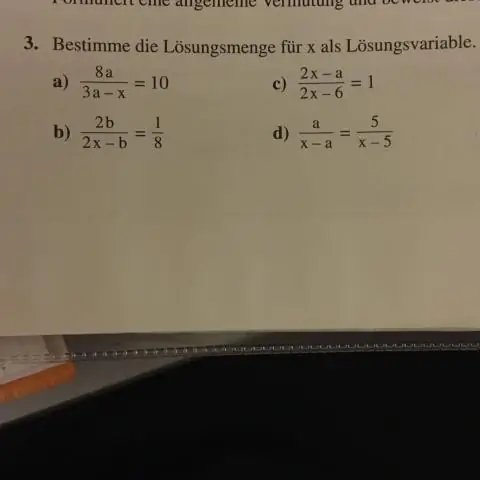
'n Stel is 'n ongeordende versameling van verskillende elemente. 'n Stel kan eksplisiet geskryf word deur sy elemente te lys met behulp van stelhakie. As die volgorde van die elemente verander word of enige element van 'n stel herhaal word, maak dit geen veranderinge in die stel
Wat is diskrete waarde?
Diskrete data kan slegs spesifieke waardes aanneem. Daar kan moontlik 'n oneindige aantal van daardie waardes wees, maar elkeen is afsonderlik en daar is geen grys area tussenin nie. Diskrete data kan numeries wees -- soos getalle van appels -- maar dit kan ook kategories wees -- soos rooi of blou, orman of vroulik, of goed of sleg