Video: Watter rotasie sal 'n gereelde seshoek op homself karteer?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Daar is 6 hoeke tussen naburige hoekpunte, hulle is almal gelyk (omdat a seshoek is gereeld ) en hul som is 360°. Dus het elke hoek 'n maat van 360°/6=60°. Elke daaropvolgende rotasie ook met 60° kaarte a seshoek op homself.
Net so, watter rotasie sal 'n Nonagon op homself karteer?
Vir 'n gereelde niehoekig , Dit kaarte op homself 9 keer tydens 'n rotasie van 360°. 'n Vorm is gesê het rotasie simmetrie as dit kaarte op homself onder rotasie ongeveer 'n punt in sy middelpunt. Die volgorde van rotasie simmetrie is die aantal kere die vorm kaarte op homself tydens a rotasie van 360°.
Weet ook watter rotasies, indien enige, die figuur op homself karteer? 'n Figuur in die vliegtuig het rotasie simmetrie as die figuur gekarteer kan word op homself deur 'n rotasie tussen 0° en 360° om die middel van die figuur . Daar is geen manier om dit te draai figuur en het dit kaart op homself . Dit het dus nie rotasie simmetrie.
Dienooreenkomstig, watter rotasie sal 'n Pentagon op homself dra?
Dit is omdat die gereelde vyfhoek rotasiesimmetrie het, en egin{align*}72^circend{align*} is die minimum aantal grade jy kan die vyfhoek draai om dit op homself te dra.
Wat is die kleinste aantal grade wat nodig is om 'n gereelde seshoek op homself te draai?
Een rotasie het 360 grade. Sedert gewone Pentagon het 5 kante en elkeen van hulle neem 360/5 = 72 grade as ons vanaf die middel gekyk word, as ons gereelde Pentagon deur draai 72 grade sal ons dieselfde vorm kry as waarvan ons begin het. Daarom is antwoord 72 grade.
Aanbeveel:
Watter transformasie dra die gelyksydige driehoek op homself?
Dra die gelyksydige driehoek op homself. So, dit is die korrekte rotasie-antwoordkeuses: rotasie van 120° antikloksgewys. rotasie van 120° kloksgewys
Wat is die formule vir die berekening van spesifieke rotasie vanaf waargenome rotasie?
Om 'n waargenome rotasie na spesifieke rotasie om te skakel, deel die waargenome rotasie deur die konsentrasie in g/mL en die padlengte in desimeters (dm)
Is optiese rotasie en spesifieke rotasie dieselfde?
In chemie is spesifieke rotasie ([α]) 'n eienskap van 'n chirale chemiese verbinding. As 'n verbinding in staat is om die polarisasievlak van vlak-gepolariseerde lig te draai, word gesê dat dit "opties aktief" is. Spesifieke rotasie is 'n intensiewe eienskap, wat dit onderskei van die meer algemene verskynsel van optiese rotasie
Watter van die vierhoek is 'n gereelde vierhoek?
Vierkantig
Hoe karteer seismiese golwe die aarde se binneland?
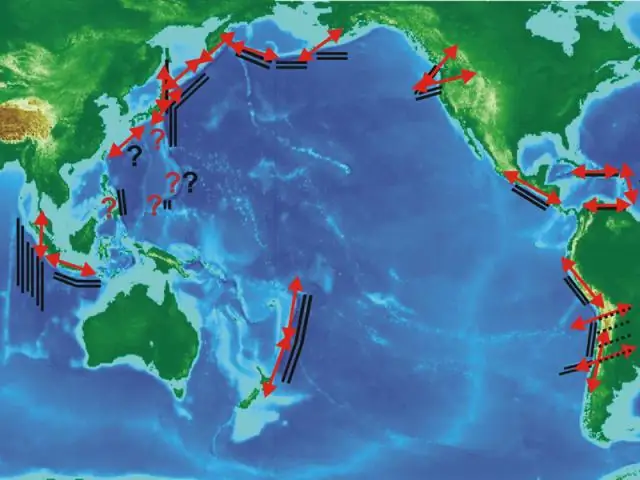
Kernstruktuur Seismologie help ons om die afmetings van die binneste en buitenste kern van die Aarde uit te werk. Omdat die spoed van die seismiese golwe van digtheid afhang, kan ons die reistyd van seismiese golwe gebruik om verandering in digtheid met diepte te karteer en te wys dat die Aarde uit verskeie lae bestaan