Video: Wat is die voorwaartse fase van die ryverminderingsproses?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Die spilpuntposisies in 'n matriks word heeltemal bepaal deur die posisies van die voorste inskrywings in die nie-nul-rye van enige echelonvorm verkry vanaf die matriks . Verminder a matriks na echelonvorm word die voorwaartse fase van die ryverminderingsproses genoem.
Gevolglik, wat is die ryverminderingsalgoritme?
Gaussiese eliminasie, ook bekend as ry vermindering , is 'n algoritme in lineêre algebra om 'n stelsel lineêre vergelykings op te los. Dit word gewoonlik verstaan as 'n reeks bewerkings wat op die ooreenstemmende matriks van koëffisiënte uitgevoer word. Die metode is vernoem na Carl Friedrich Gauss (1777–1855).
Behalwe hierbo, wat is elementêre rybewerkings van matrikse? Elementêre bedrywighede Vermenigvuldig elke element in a ry (of kolom) deur 'n nie-nul getal. Vermenigvuldig a ry (of kolom) deur 'n nie-nul getal en voeg die resultaat by 'n ander ry (of kolom).
Weet ook, is die ryverminderingsalgoritme slegs van toepassing op vergrote matrikse?
Die ryverminderingsalgoritme is slegs van toepassing op vergrote matrikse vir 'n lineêre stelsel. Antwoord: Onwaar. Enige matriks kan wees verminder . As een ry in 'n echelon vorm van 'n vermeerderde matriks is [0 0 0 5 0], dan is die geassosieerde lineêre stelsel inkonsekwent.
Kan jy ry verminder voordat jy determinant vind?
Determinant van 'n boonste (onderste) driehoekige of diagonale matriks is gelyk aan die produk van sy diagonale inskrywings. detA =detAT, so ons kan óf toepas ry of kolombewerkings om die te kry determinant . 2. As twee rye of twee kolomme van A is identies of as A het 'n ry of 'n kolom van nulle, dan is detA = 0.
Aanbeveel:
Is die voorwaartse reaksie endotermies of eksotermies?
Die voorwaartse reaksie het ΔH>0. Dit beteken dat die voorwaartse reaksie endotermies is. Die omgekeerde reaksie moet dus eksotermies wees
Wat is die naam van die chemiese stof waar die energie tydens die eerste fase van fotosintese gestoor word?
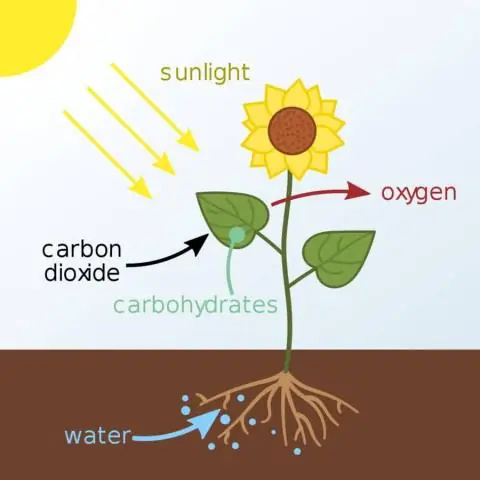
Die ligafhanklike reaksies gebruik ligenergie om twee molekules te maak wat nodig is vir die volgende stadium van fotosintese: die energiebergingsmolekule ATP en die gereduseerde elektrondraer NADPH. By plante vind die ligreaksies plaas in die tilakoïedmembrane van organelle wat chloroplaste genoem word
Wat is die naam van die ensiem wat die sintese van die mRNA-streng kataliseer?
MRNA is "boodskapper" RNA. mRNA word in die kern gesintetiseer deur die nukleotiedvolgorde van DNA as 'n sjabloon te gebruik. Hierdie proses vereis nukleotiedtrifosfate as substrate en word deur die ensiem RNA-polimerase II gekataliseer. Die proses om mRNA van DNA te maak, word transkripsie genoem, en dit vind in die kern plaas
Hoe kan jy weet of 'n voorwaartse of terugwaartse reaksie bevoordeel word?
Indien K K, word die reaktante bevoordeel. As Q < K, word die produkte bevoordeel
Watter fase van meiose I stem die meeste ooreen met die vergelykbare fase in mitose?
Sleutelbordkortpaaie vir die gebruik van flitskaarte: watter van die volgende is nie 'n duidelike kenmerk van meiose nie? aanhegting van susterkinetochore aan spilmikrobuisies watter fase van meiose I is die meeste soortgelyk aan die vergelykbare fase in mitose? telofase I