Video: Hoe hou families van funksieparameters en die beskrywings van grafieke verband?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Funksie families is groepe van funksies met ooreenkomste wat dit makliker maak om grafiek wanneer jy vertroud is met die ouer funksie , die mees basiese voorbeeld van die vorm. A parameter is 'n veranderlike in 'n algemene vergelyking wat 'n spesifieke waarde aanneem om 'n spesifieke vergelyking te skep.
Wat het grafieke binne 'n familie van funksies dan in gemeen?
A familie van funksies is 'n stel van funksies wie se vergelykings het 'n soortgelyke vorm. Die "ouer" van die familie is die vergelyking in die familie met die eenvoudigste vorm. Byvoorbeeld, y = x2 is 'n ouer vir ander funksies , soos y = 2x2 - 5x + 3.
Weet ook, wat is die 4 tipes funksies? Daar kan 4 verskillende tipes gebruikergedefinieerde funksies wees, dit is:
- Funksie met geen argumente en geen terugkeerwaarde.
- Funksie met geen argumente en 'n terugkeerwaarde.
- Funksie met argumente en geen terugkeerwaarde nie.
- Funksie met argumente en 'n terugkeerwaarde.
Wat dit betref, wat is die 4 ouerfunksies?
Hierdie elementêre funksies rasionele insluit funksies , eksponensiële funksies , basiese polinome, absolute waardes en die vierkantswortel funksie.
Wat is die 6 funksies van die gesin?
- Byvoeging van nuwe lede. • Gesinne kry kinders deur geboorte, aanneming, en kan ook die hulp van vrugbaarheidsklinieke, ens.
- Fisiese versorging van lede. •
- Sosialisering van kinders. •
- Maatskaplike beheer van lede. •
- Affektiewe Versorging- Handhawing van Lede se moreel. •
- Die vervaardiging en verbruik van goedere en dienste. •
Aanbeveel:
Hoe hou die struktuur van koolstof verband met die verskeidenheid makromolekules wat in lewende dinge voorkom?
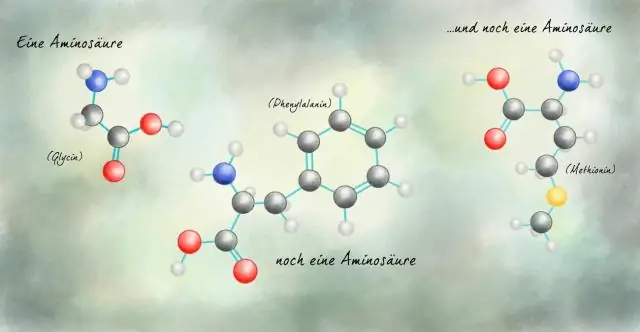
Die koolstofatoom het unieke eienskappe wat dit toelaat om kovalente bindings aan soveel as vier verskillende atome te vorm, wat hierdie veelsydige element ideaal maak om as die basiese strukturele komponent, of "ruggraat" van die makromolekules te dien
Hoe het organiese verbindings hul naam gekry. Hoe hou die woord verband met sy betekenis?
Hoe hou die woord verband met sy betekenis? Organiese verbindings kry sy naam van die aantal koolstofbindings. Die woord hou verband met die betekenis omdat dit te doen het met bindings in koolstofatome in organiese verbindings
Hoe dink jy hou die samehangende aard van water verband met die verdamping daarvan?
Kohesie van water Voordat dit oorloop, vorm die water 'n koepelagtige vorm bo die rand van die glas. Kohesie verwys na die aantrekking van molekules vir ander molekules van dieselfde soort, en watermolekules het sterk kohesiekragte danksy hul vermoë om waterstofbindings met mekaar te vorm
Hoe hou die struktuur van die vakuool verband met sy funksie?
Vakuole is membraangebonde sakkies binne die sitoplasma van 'n sel wat op verskeie maniere funksioneer. In volwasse plantselle is vakuole geneig om baie groot te wees en is dit uiters belangrik in die verskaffing van strukturele ondersteuning, sowel as om funksies te dien soos berging, afvalverwydering, beskerming en groei
Hoe hou die aftrekking van heelgetalle verband met die optel van heelgetalle?
Antwoord en verduideliking: Om heelgetalle op te tel beteken om heelgetalle met dieselfde tekens by te tel, terwyl heelgetalle aftrek beteken om die heelgetalle van teenoorgestelde tekens op te tel