Video: Waarom word vektore in masjienleer gebruik?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
In Masjienleer , kenmerk vektore word gebruik om numeriese of simboliese kenmerke, genoem kenmerke, van 'n voorwerp op 'n wiskundige, maklik analiseerbare manier voor te stel. Hulle is belangrik vir baie verskillende areas van Masjienleer en patroonverwerking.
Net so, wat is 'n vektor in masjienleer?
Vektor , of dit nou in is Masjienleer of Lineêre Algebra verwys na dieselfde - 'n versameling / skikking van getalle - voorbeeld: [1, 3, 2] is 'n vektor . In Masjienleer hierdie vektor word 'n kenmerk genoem vektor aangesien elkeen van hierdie waardes ooreenstem met sommige kenmerke, byvoorbeeld kenmerke van 'n vrug in 'n vrugklassifikasieprobleem.
Boonop, hoekom is Lineêre Algebra belangrik vir masjienleer? Matriks faktorisering is 'n sleutelinstrument in Lineêre algebra en word wyd gebruik as 'n element van baie meer komplekse bewerkings in beide Lineêre algebra (soos die matriks inverse) en Masjienleer (Minste vierkante). Om hoër-orde te lees en te interpreteer matriks bedrywighede, moet jy verstaan matriks faktorisering.
Om ook te weet, wat is 'n vektor in ML?
Hoekom word matrikse met dimensies Nx1 genoem vektore As jy enige fisika of ingenieurswese op universiteitsvlak geneem het, dink jy waarskynlik aan vektore as iets wat beide grootte en rigting het waar die lengte van die vektor is die grootte en die oriëntasie van die vektor is die rigting.
Wat is kenmerk in masjienleer?
In Masjienleer en patroonherkenning, a kenmerk is 'n individuele meetbare eienskap of kenmerk van 'n verskynsel wat waargeneem word. Die konsep van" kenmerk " is verwant aan dié van verklarende veranderlike wat gebruik word instatistiese tegnieke soos lineêre regressie.
Aanbeveel:
Waarom word die Ames-toets vir mutagene gebruik om vir karsinogene MCAT te toets?
Die vraag vra die eksaminator om te verduidelik waarom die Ames-toets vir mutagene gebruik kan word om vir karsinogene te toets. In die Ames-toets is die chemikalieë wat mutasies in Salmonella-toetsstamme veroorsaak moontlik karsinogene, as gevolg van die feit dat hulle DNA muteer en DNA-mutasies kan kanker veroorsaak (B)
Waarom word Fourier-reekse in kommunikasie-ingenieurswese gebruik?
Kommunikasie-ingenieurswese handel hoofsaaklik oor seine en dus is seine van verskillende soorte soos voortgaan, diskrete, periodiek, nie-periodiek en baie van baie tipes. NouFourier-transformasie help ons om tyddomeinsein in frekwensiedomein te omskep. Omdat dit ons toelaat om die frekwensiekomponente van 'n sein te onttrek
Waarom word aanwyser nie in kmno4-titrasie gebruik nie?
Waarom word 'n aanwyser nie gebruik in die titrasie van kaliumpermanganaat met oksaalsuur nie? Die kleur van die permanganaat IS die aanwyser. Die eerste druppel oortollige MnO4- sal 'n permanente pienk kleur aan die reaksie-oplossing gee-so daar is geen behoefte aan 'n bykomende indikator
Wat is ewekansige stap in masjienleer?
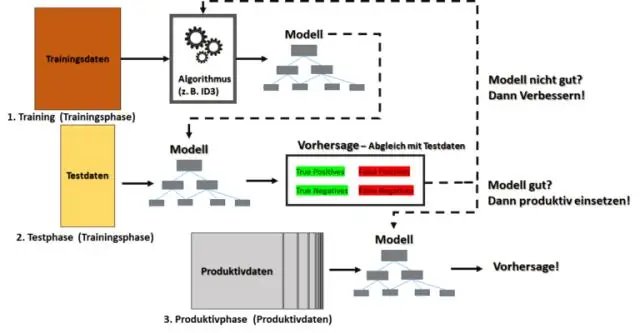
A: In masjienleer kan 'n 'random walk'-benadering op verskeie maniere toegepas word om die tegnologie te help om deur die groot opleidingsdatastelle te sif wat die basis bied vir die masjien se uiteindelike begrip. 'n Ewekansige stap, wiskundig, is iets wat op verskeie verskillende tegniese maniere beskryf kan word
Wat is die vergelyking wat gebruik word om die totale hoeveelheid energie wat deur 'n toestel gebruik word te bereken?
Die formule wat energie en krag verbind is: Energie = Drywing x Tyd. Die eenheid van energie is die joule, die eenheid van krag is die watt, en die eenheid van tyd is die tweede