Video: Wat is die sluitingswet van optelling?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Sluiting . Sluiting is wanneer 'n operasie (soos " byvoeging ") op lede van 'n versameling (soos "reële getalle") maak altyd 'n lid van dieselfde versameling. So die resultaat bly in dieselfde versameling.
Op hierdie manier, wat is sluiting onder toevoeging?
So 'n stel is gesluit onder toevoeging as die som van enige twee elemente in die versameling ook in die versameling is. Byvoorbeeld, die reële getalle R het 'n standaard binêre bewerking wat genoem word toevoeging (die bekende). Dan is die versameling heelgetalle Z gesluit onder toevoeging want die som van enige twee heelgetalle is 'n heelgetal.
Verder, wat is sluitingseiendom met voorbeeld? Dus, 'n stel het of ontbreek sluiting met betrekking tot 'n gegewe operasie. Vir voorbeeld , die versameling ewe natuurlike getalle, [2, 4, 6, 8,…], word gesluit met betrekking tot optelling omdat die som van enige twee van hulle 'n ander ewe natuurlike getal is, wat ook 'n lid van die versameling is.
As u dit in die oog hou, wat is sluitingswet?
Sluiting beskryf die geval wanneer die resultate van 'n wiskundige bewerking altyd gedefinieer word. Byvoorbeeld, in gewone rekenkunde het optelling sluiting . Wanneer 'n mens twee getalle bytel, is die antwoord 'n getal. In die natuurlike getalle het aftrekking nie sluiting , maar in die heelgetalle het aftrekking wel sluiting.
Wat is die eienskappe van optelling?
Eienskappe van toevoeging. Daar is vier wiskundige eienskappe wat optelling behels. Die eiendomme is die kommutatief , assosiatief , toevoeging identiteit en verspreidingseienskappe. Byvoeging Identiteit Eienskap: Die som van enige getal en nul is die oorspronklike getal.
Aanbeveel:
Watter reaksies is syn-optelling?
Syn-optelling: 'n Addisiereaksie waarin alle nuwe bindings op dieselfde oppervlak van die reaktantmolekule gevorm word. Hierdie hidroborasie-oksidasiereaksie is 'n sin-byvoeging omdat hierdie reaksie 'n H en OH aan dieselfde vlak van die alkeen lewer
Wat is die naam van die chemiese stof waar die energie tydens die eerste fase van fotosintese gestoor word?
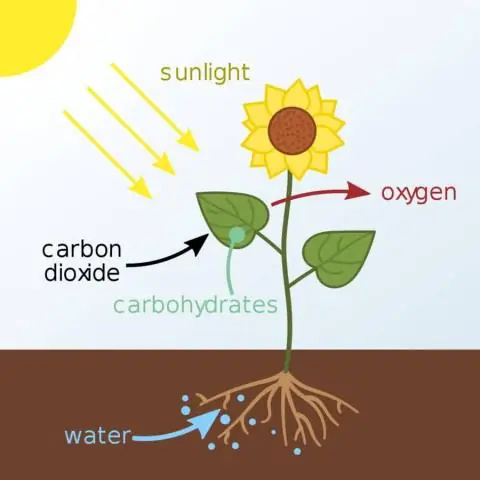
Die ligafhanklike reaksies gebruik ligenergie om twee molekules te maak wat nodig is vir die volgende stadium van fotosintese: die energiebergingsmolekule ATP en die gereduseerde elektrondraer NADPH. By plante vind die ligreaksies plaas in die tilakoïedmembrane van organelle wat chloroplaste genoem word
Wat is die korrekte volgorde van die ekologiese hiërargie van die kleinste na die grootste?
Opsomming Vlakke van organisasie in ekologie sluit die bevolking, gemeenskap, ekosisteem en biosfeer in. 'n Ekosisteem is al die lewende dinge in 'n gebied wat in wisselwerking is met al die abiotiese dele van die omgewing
Hoe verduidelik jy optelling?
Optelling is die term wat gebruik word om twee of meer getalle saam te beskryf. Die plusteken '+' word gebruik om 'n optelling aan te dui: 2 + 2. Die + kan verskeie kere gebruik word soos vereis: 2 + 2 + 2. Vir langer lyste getalle is dit gewoonlik makliker om die getalle in 'n kolom te skryf en die berekening uit te voer die onderkant
Wat is die naam van die ensiem wat die sintese van die mRNA-streng kataliseer?
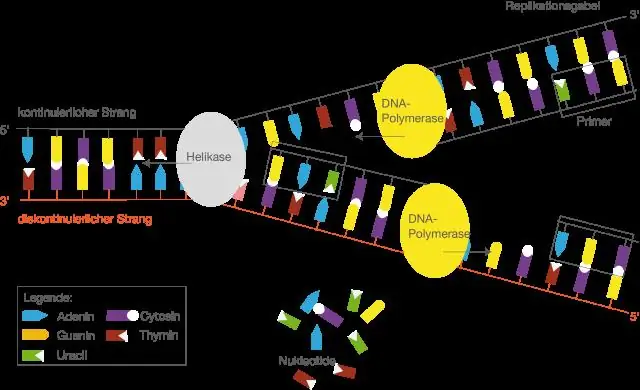
MRNA is "boodskapper" RNA. mRNA word in die kern gesintetiseer deur die nukleotiedvolgorde van DNA as 'n sjabloon te gebruik. Hierdie proses vereis nukleotiedtrifosfate as substrate en word deur die ensiem RNA-polimerase II gekataliseer. Die proses om mRNA van DNA te maak, word transkripsie genoem, en dit vind in die kern plaas