Video: Wat sê Chebyshev se ongelykheid?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Chebyshev se ongelykheid sê dat ten minste 1-1/K2 van data van 'n steekproef moet binne K standaardafwykings van die gemiddelde val (hier K is enige positiewe reële getal groter as een). Maar as die datastel is nie in die vorm van 'n klokkurwe versprei word nie, dan kan 'n ander hoeveelheid binne een standaardafwyking wees.
Wat meet Chebyshev se ongelykheid dienooreenkomstig?
Chebyshev se ongelykheid (ook bekend as Tchebysheff's ongelykheid ) is 'n meet van die afstand vanaf die gemiddelde van 'n ewekansige datapunt in 'n stel, uitgedruk as 'n waarskynlikheid. Dit stel dat vir 'n datastel met 'n eindige variansie, die waarskynlikheid dat 'n datapunt binne k standaardafwykings van die gemiddelde lê, 1/k is2.
Ook, wat is Chebyshev se stellingformule? Chebyshev se stelling state vir enige k > 1, ten minste 1-1/k2 van die data lê binne k standaardafwykings van die gemiddelde. Soos gesê, moet die waarde van k groter as 1 wees. Deur dit te gebruik formule en as ons die waarde 2 inprop, kry ons 'n resulterende waarde van 1-1/22, wat gelyk is aan 75%.
As jy dit in ag neem, hoe bewys jy Chebyshev se ongelykheid?
Een manier om Chebyshev se ongelykheid te bewys is om Markov's toe te pas ongelykheid na die ewekansige veranderlike Y = (X − Μ)2 met a = (kσ)2. Chebyshev se ongelykheid dan volg deur te deel deur k2σ2.
Wat is Chebyshev se stelling en hoe word dit gebruik?
Chebyshev se stelling is gebruik word om die proporsie waarnemings te vind wat jy sou verwag om te vind binne twee standaardafwykings van die gemiddelde. Chebyshev s'n Interval verwys na die intervalle wat jy wil vind wanneer jy die stelling . Byvoorbeeld, jou interval kan van -2 tot 2 standaardafwykings van die gemiddelde wees.
Aanbeveel:
Hoe vind jy die snysels van 'n ongelykheid?
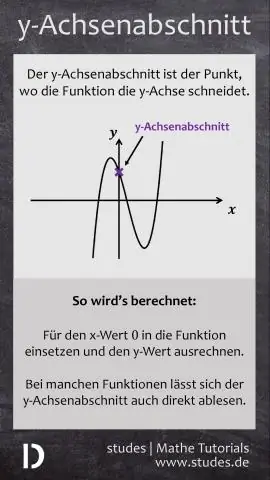
Alternatiewelik kan ons die x-afsnit en die y-afsnit van die standaardvorm lineêre gelykheid bepaal deur y = 0 te vervang, dan vir x op te los en x = 0 te vervang, dan onderskeidelik vir y op te los. Onthou dat die x-afsnit die waarde van x is wanneer y = 0 en hulle-afsnit die waarde van y is wanneer x = 0
Hoe skaker jy die streek van 'n ongelykheid?
Daar is drie stappe: Herrangskik die vergelyking sodat 'y' aan die linkerkant is en al die ander aan die regterkant. Teken die 'y='-lyn (maak dit 'n soliede lyn vir y≤ of y≥, en 'n stippellyn vir y) Skakering bo die lyn vir 'n 'groter as' (y> of y≥) of onder die lyn vir 'n 'minder as' (y< of y≤)
Hoe bepaal jy of 'n ongelykheid geen oplossing het nie?
Isoleer die absolute waarde-uitdrukking aan die linkerkant van die ongelykheid. As die getal aan die ander kant van die ongelykheidsteken negatief is, het jou vergelyking óf geen oplossing nie óf alle reële getalle as oplossings. Gebruik die teken van elke kant van jou ongelykheid om te besluit watter van hierdie gevalle geld
Is HDI verantwoordelik vir ongelykheid?
Terwyl die HDI beskou kan word as 'n indeks van "potensiële" menslike ontwikkeling wat verkry kan word as prestasies gelykop verdeel word, is die IHDI die werklike vlak van menslike ontwikkeling (wat verantwoordelik is vir ongelykheid in die verspreiding van prestasies oor mense in 'n samelewing)
Hoe skryf jy die domein van 'n ongelykheid?
As 'n ongelykheid, sou ons Lees skryf as 'die domein van die funksie is alle waardes van x wat groter as of gelyk aan nul is'. Vir meer oor ongelykhede sien Ongelykhede. In sogenaamde intervalnotasie het dieselfde funksie 'n domein van Dit beskryf die stel waardes van 0 tot positiewe oneindigheid