Video: Wat is 'n voorbeeld van 'n rasionale getal wat nie 'n heelgetal is nie?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
'n rasioneel ” nommer is die verhouding tussen twee heelgetalle. Vir voorbeeld , die volgende is rasionale getalle , en nie een van hulle is 'n heelgetal nie: 1 / 2. 2 / 3.
Die vraag is ook, wat is 'n rasionale getal wat nie 'n heelgetal is nie?
Alle negatiewe heelgetalle is rasionale getalle maar die is nie heelgetalle nie . Byvoorbeeld -3 is a rasionale getal (kan uitgedruk word as -3/1), maar dit is nie 'n heelgetal nie . Die breuke soos 1/2, -3/4, 22/7 ens.
Tweedens, is negatiewe 3 'n rasionale getal? − 3 is negatief dit is dus nie 'n natuurlike of geheel nie nommer . Rasionale getalle is getalle wat uitgedruk kan word as 'n breuk of verhouding van twee heelgetalle. Rasionale getalle word aangedui as Q. Sedert - 3 kan geskryf word as − 3 1, kan daar geargumenteer word dat − 3 is ook 'n ware nommer.
Tweedens, wat is 'n rasionale getal wat 'n heelgetal is?
Elke heelgetal is 'n rasionale getal : byvoorbeeld, 3=31. So dit is rasioneel . Elke heelgetal n kan geskryf word as 'n breuk van heelgetalle: n=n1. Ons is nie verplig om dit so te skryf nie; ons moet net weet dat dit moontlik is om elke uit te druk heelgetal as 'n breuk van heelgetalle, en daarom is dit rasioneel.
Kan 'n rasionale getal 'n heelgetal wees, maar nie 'n heelgetal nie?
Stel van heelgetalle = {0, 1, 2, 3, 4, …} Heelgetalle is net heelgetalle wat nie-negatief is nie. Met behulp van stelnotasie, ons kan sê dat die stel van heelgetalle is terwyl die stel van heelgetalle is basies. So om terug te kom na die vraag; Geen , daar is geen rasionale getal wat nie 'n heelgetal is nie maar is 'n heelgetal.
Aanbeveel:
Wat is natuurlike getal en heelgetal met voorbeeld?
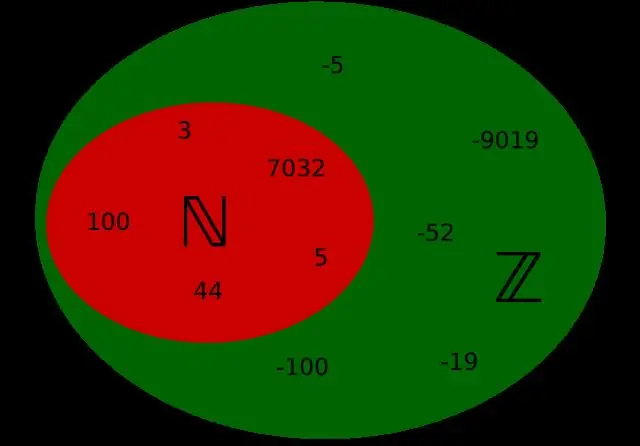
Natuurlike getalle is almal getalle 1, 2, 3, 4 … Dit is die getalle wat jy gewoonlik tel en hulle sal voortgaan tot in oneindigheid. Heelgetalle is alle natuurlike getalle insluitend 0 bv. 0, 1, 2, 3, 4… Heelgetalle sluit alle heelgetalle en hul negatiewe eweknie in, bv.
Is elke natuurlike getal 'n heelgetal?
Ja dit is waar. Omdat natuurlike getalle begin by 1 en eindig in oneindig waar heelgetalle begin by 0 en eindig in oneindig. 0 is die enigste getal wat in heelgetalle is, maar nie in natuurlike getalle nie. Daarom is elke natuurlike getal 'n heelgetal
Is 4.14 'n rasionale getal?
Hierdie getal is nie reeds as 'n breuk geskryf nie; dit kan egter as 'n breuk herskryf word. Die antwoord is dat omdat -4 geskryf kan word as die verhouding van -4 tot 1, dit 'n berekeningsgetal is
Hoe is 7 'n rasionale getal?
Elke heelgetal is 'n rasionale getal, aangesien elke heelgetal n in die vorm n/1 geskryf kan word. Byvoorbeeld 5 = 5/1 en dus is 5 'n rasionale getal. Getalle soos 1/2, 45454737/2424242 en -3/7 is egter ook rasionaal, aangesien dit breuke is waarvan die teller en noemer heelgetalle is
Is 0 'n rasionale getal of nie?
Ja nul is 'n rasionale getal. Ons weet dat die heelgetal 0 in enige een van die volgende vorms geskryf kan word. Byvoorbeeld, 0/1, 0/-1, 0/2, 0/-2, 0/3, 0/-3, 0/4, 0/-4 ensovoorts …. Dus kan 0 geskryf word as, waar a/b = 0, waar a = 0 en b enige nie-nul heelgetal is