INHOUDSOPGAWE:
Video: Wat is die area van 'n kardioïed?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Vind die gebied binne die kardioïed r = 1 + cos θ. Beantwoord die kardioïed word so genoem omdat dit hartvormig is. Deur radiale strepe te gebruik, is die grense van integrasie (binne) r van 0 tot 1 + cos θ; (buitenste) θ van 0 tot 2π. Sodat die gebied is. 2π 1+cos θ dA = r dr dθ.
Verder, hoe vind jy die area van 'n poolgebied?
Die oppervlakte van 'n gebied in poolkoördinate gedefinieer deur die vergelyking r=f(θ) met α≦θ≦β word gegee deur die integraal A=1 2 ∫βα[f(θ)] 2 dθ. Om die area tussen te vind twee krommes in die poolkoördinaatstelsel, vind eers die snypunte en trek dan die ooreenstemmende oppervlaktes af.
Mens kan ook vra, hoe integreer jy Cos 2x? Die integrale van cos ( 2x ) is (1/2)sonde( 2x ) + C, waar C 'n konstante is.
Hiervan, wat is die formule vir oppervlakte onder 'n kromme?
Die area onder 'n kromme tussen twee punte word uitgevind deur 'n definitiewe integraal tussen die twee punte te doen. Om die gebied onder die kromme y = f(x) tussen x = a & x = b, integreer y = f(x) tussen die limiete van a en b. Hierdie gebied kan bereken word deur integrasie met gegewe limiete te gebruik.
Hoe los jy parametriese vergelykings op?
Voorbeeld 1:
- Vind 'n stel parametriese vergelykings vir die vergelyking y=x2+5.
- Ken enige een van die veranderlikes gelyk aan t toe. (sê x = t).
- Dan kan die gegewe vergelyking herskryf word as y=t2+5.
- Daarom is 'n stel parametriese vergelykings x = t en y=t2+5.
Aanbeveel:
Wat is die naam van die chemiese stof waar die energie tydens die eerste fase van fotosintese gestoor word?
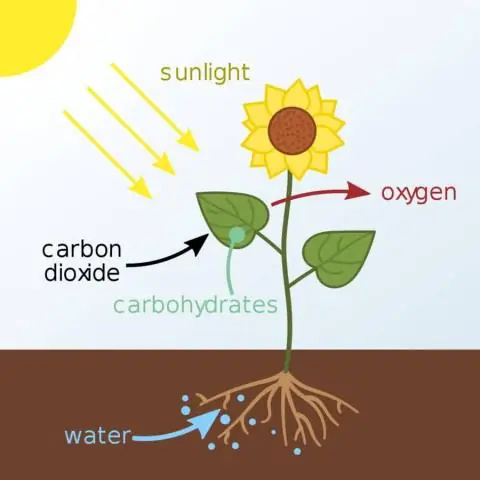
Die ligafhanklike reaksies gebruik ligenergie om twee molekules te maak wat nodig is vir die volgende stadium van fotosintese: die energiebergingsmolekule ATP en die gereduseerde elektrondraer NADPH. By plante vind die ligreaksies plaas in die tilakoïedmembrane van organelle wat chloroplaste genoem word
Wat is die korrekte volgorde van die ekologiese hiërargie van die kleinste na die grootste?
Opsomming Vlakke van organisasie in ekologie sluit die bevolking, gemeenskap, ekosisteem en biosfeer in. 'n Ekosisteem is al die lewende dinge in 'n gebied wat in wisselwerking is met al die abiotiese dele van die omgewing
Wat suggereer die verspreiding van die seebodem op die ouderdom van die seebodem?
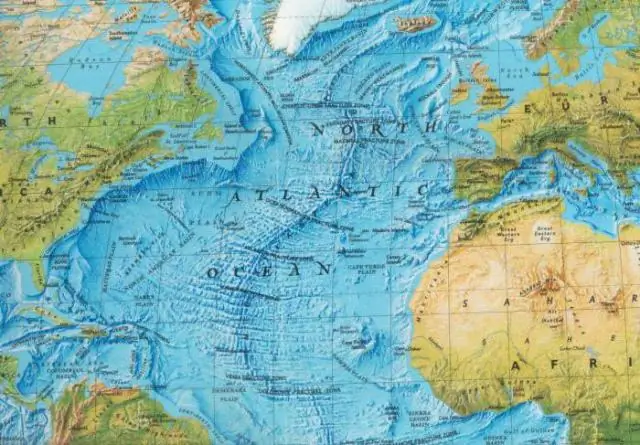
Die jongste kors van die seebodem kan gevind word naby die seebodemverspreidingsentrums of middel-oseaan-rante. Soos die plate uitmekaar skei, styg magma van onder die aarde se oppervlak af om die leë leemte in te vul. In wese is oseaniese plate meer vatbaar vir subduksie namate hulle ouer word
Wat is die naam van die ensiem wat die sintese van die mRNA-streng kataliseer?
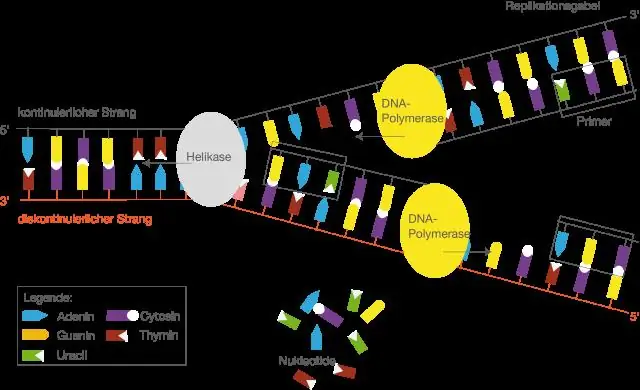
MRNA is "boodskapper" RNA. mRNA word in die kern gesintetiseer deur die nukleotiedvolgorde van DNA as 'n sjabloon te gebruik. Hierdie proses vereis nukleotiedtrifosfate as substrate en word deur die ensiem RNA-polimerase II gekataliseer. Die proses om mRNA van DNA te maak, word transkripsie genoem, en dit vind in die kern plaas
Hoe vind jy die area van die gesig deur die oppervlakte te gebruik?
Oppervlakte is die som van die oppervlaktes van alle vlakke (of oppervlaktes) op 'n 3D-vorm. 'n Kubus het 6 reghoekige vlakke. Om die oppervlakte van 'n blokkie te vind, voeg die oppervlaktes van al 6 vlakke by. Ons kan ook die lengte (l), breedte (w) en hoogte (h) van die prisma benoem en die formule, SA=2lw+2lh+2hw, gebruik om die oppervlakte te vind