Video: Wat is die verskil tussen lineêre eksponensiële en kwadratiese?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Lineêr , eksponensieel en kwadraties funksies kan gebruik word om werklike verskynsels te modelleer. Algebraïes, lineêr funksies is polinoomfunksies met 'n hoogste eksponent van een, eksponensiële funksies het 'n veranderlike in die eksponent, en kwadraties funksies is polinoomfunksies met 'n hoogste eksponent van twee.
Behalwe dit, wat is lineêre kwadraties en eksponensieel?
As die eerste verskil dieselfde waarde is, sal die model wees lineêr . As die tweede verskil dieselfde waarde is, sal die model wees kwadraties . As die aantal kere wat die verskil geneem is voordat herhaalde waardes gevind is vyf oorskry, kan die model wees eksponensiële of 'n ander spesiale vergelyking.
Tweedens, wat is lineêre en eksponensiële funksies? Lineêre funksies is reguit lyne terwyl eksponensiële funksies is geboë lyne. As dieselfde getal by y gevoeg word, dan is die funksie het 'n konstante verandering en is lineêr . As die y-waarde met 'n sekere persentasie toeneem of afneem, dan is die funksie is eksponensiële.
Ook om te weet is, wat is die verskil tussen lineêr en eksponensieel?
Lineêr funksies verander teen 'n konstante tempo per eenheidsinterval. An eksponensiële funksie verander deur 'n gemeenskaplike verhouding oor gelyke intervalle.
Hoe bepaal jy of 'n funksie lineêr is?
A lineêre funksie is in die vorm y = mx + b of f(x) = mx + b, waar m die helling of tempo van verandering is en b die y-afsnit is of waar die grafiek van die lyn die y-as kruis. Jy sal agterkom dat dit funksie is graad 1 wat beteken dat die x-veranderlike 'n eksponent van 1 het.
Aanbeveel:
Hoe is die oplossing van lineêre ongelykhede en lineêre vergelykings soortgelyk?
Die oplossing van lineêre ongelykhede is baie soortgelyk aan die oplossing van lineêre vergelykings. Die belangrikste verskil is dat u die ongelykheidsteken omdraai wanneer u met 'n negatiewe getal deel of vermenigvuldig. Die grafiek van lineêre ongelykhede het nog 'n paar verskille. Die deel wat ingekleur is, sluit die waardes in waar die lineêre ongelykheid waar is
Wat is die verskil tussen die massa van 'n proton en die massa van 'n elektron?
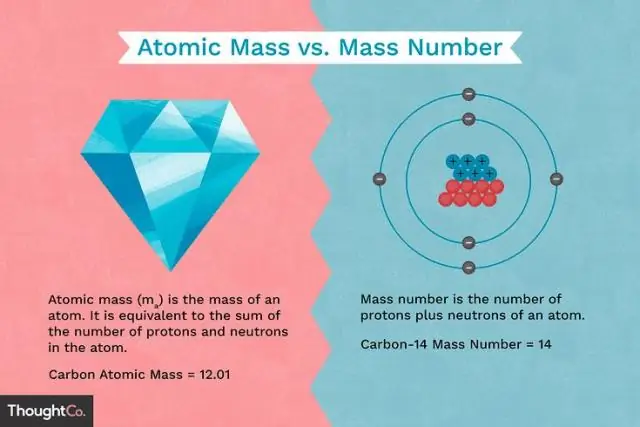
Protone en neutrone het ongeveer dieselfde massa, maar hulle is albei baie meer massief as elektrone (ongeveer 2 000 keer so massief soos 'n elektron). Die positiewe lading op 'n proton is gelyk aan die negatiewe lading op 'n elektron
Wat is die verskil tussen die puriene en die pirimidiene?
Die puriene in DNA is adenien en guanien, dieselfde as in RNA. Die pirimidiene in DNS is sitosien en timien; in RNA is dit sitosien en urasil. Puriene is groter as pirimidiene omdat hulle 'n tweeringstruktuur het terwyl pirimidiene net 'n enkele ring het
Wat is die verskil tussen logistieke en eksponensiële groei?
Beide modelle verwys na die bevolking maar op verskillende maniere. Een groot verskil is dat eksponensiële groei stadig begin en dan optel namate die bevolking toeneem, terwyl logistieke groei vinnig begin, dan vertraag nadat die drakrag bereik is
Wat is die basiese verskil tussen lineêre kombinasies kontraste en veelvuldige vergelykings?
6. (2 punte) Wat is die basiese verskil tussen lineêre kombinasies (kontraste) en veelvuldige vergelykings? Lineêre kombinasies is beplande vergelykings; dit wil sê, bepaalde middele word op verskillende maniere gekombineer en gekontrasteer met ander kombinasies van middele