
- Outeur Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:33.
- Laas verander 2025-01-22 16:55.
Trapesium-middelsegmentstelling . Die driehoek middelsegment stelling stel dat die lyn wat die middelpunte verbind van twee kante van 'n driehoek, genoem die middelsegment , is parallel na die derde sy, en sy lengte is gelyk aan die helfte van die lengte van die derde sy.
Hiervan, hoe vind jy die middelsegment van 'n trapesium?
A trapesium middelsegment verbind die middelpunte van die twee kongruente sye van die trapesium , en is parallel aan die paar ewewydige sye. Die lengte van die middelsegment is die som van die twee basisse gedeel deur 2. Onthou dat die basisse van a trapesium is die twee parallelle sye.
Weet ook, hoe gebruik jy die middelsegmentstelling? Die Driehoek Middelsegmentstelling stel dat, as ons die middelpunte van enige twee kante verbind van 'n driehoek met 'n lynstuk, dan voldoen daardie lynstuk aan die volgende twee eienskappe: Die lynstuk sal parallel aan die derde sy wees. Die lengte van die lynstuk sal die helfte van die lengte van die derde sy wees.
Om ook te weet, is hoe vind jy die middelsegment?
Eenvoudig gestel, dit verdeel twee sye van 'n driehoek gelykop. Die middelpunt van 'n sy verdeel die sy in twee gelyke segmente. Soos jy kan sien in die prentjie hieronder is DE die middelsegment van die driehoek ABC. Punt D verdeel segment AB in twee gelyke dele, en punt E verdeel segment CB in twee gelyke dele.
Hoe bewys jy iets is 'n trapezium?
Een manier om te bewys dat 'n vierhoek 'n gelykbenige trapesium is, is om te wys:
- Die vierhoek het twee parallelle sye.
- Die onderste basishoeke is kongruent en die boonste basishoeke is kongruent.
Aanbeveel:
Hoe vind jy die basishoeke van 'n gelykbenige trapesium?

Die basisse (bo en onder) van 'n gelykbenige trapezium is parallel. Teenoorstaande sye van 'n gelykbenige trapezium is ewe lank (kongruent). Die hoeke aan weerskante van die basisse is dieselfde grootte/maat (kongruent)
Is die basishoeke van 'n gelykbenige trapesium kongruent?

Die basisse (bo en onder) van 'n gelykbenige trapesium is parallel. Die teenoorgestelde sye van 'n gelykbenige trapesium is ewe lank (kongruent). Die hoeke aan weerskante van die basisse is dieselfde grootte/maat (kongruent)
Wat is die naam van die ensiem wat die sintese van die mRNA-streng kataliseer?
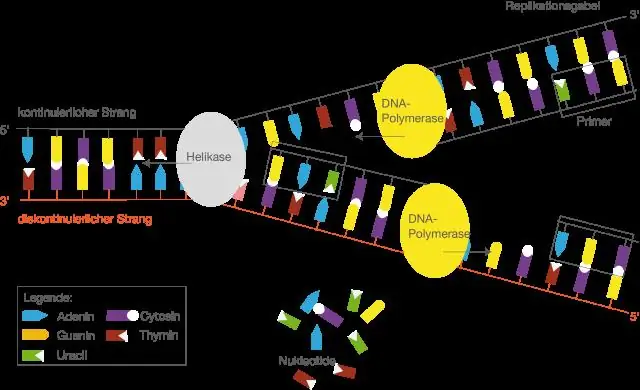
MRNA is "boodskapper" RNA. mRNA word in die kern gesintetiseer deur die nukleotiedvolgorde van DNA as 'n sjabloon te gebruik. Hierdie proses vereis nukleotiedtrifosfate as substrate en word deur die ensiem RNA-polimerase II gekataliseer. Die proses om mRNA van DNA te maak, word transkripsie genoem, en dit vind in die kern plaas
Hoe vind jy die driehoek-middelsegmentstelling?

Die Driehoek-middelsegmentstelling stel dat die lynstuk wat die middelpunte van enige twee sye van 'n driehoek verbind, die volgende eienskappe sal bevredig: Die lynstuk sal parallel aan die derde sy wees. Die lengte van die lynstuk sal die helfte van die lengte van die derde sy wees
Hoe verskil 'n trapesium van 'n vierkant?

Beide 'n vierkant en 'n trapesium bevat 4 sye en hoeke wat optel tot 360. Vierkante het gelyke sye en hoeke, dit bevat ook twee stelle teenoorstaande parallelle sye. Trapesoïede het een stel parallelle sye
