INHOUDSOPGAWE:
Video: Hoe vind jy die sentrale hoek gegewe die oppervlakte en radius van 'n sektor?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2024-01-18 08:12
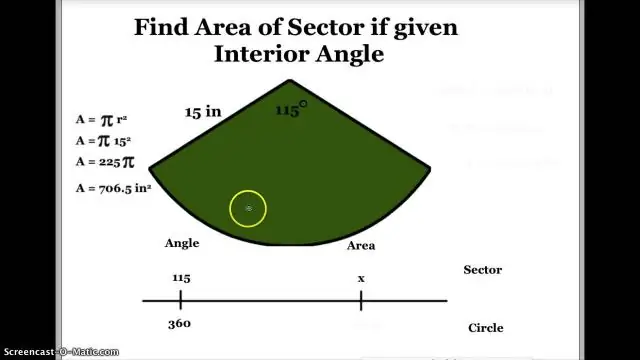
Bepaling van die sentrale hoek vanuit die sektorarea
- (πr2) × ( sentrale hoek in grade ÷ 360 grade) = sektor gebied . As die sentrale hoek word in radiale gemeet, word die formule eerder:
- sektor gebied = r2 × ( sentrale hoek in radiale ÷ 2).
- (θ ÷ 360 grade) × πr2.
- (52,3 ÷ 100π) × 360.
- (52.3 ÷ 314) × 360.
Op hierdie manier, hoe vind jy die sentrale hoek gegewe die radius?
Vind die Sentrale hoek van die Boog Lengte en Radius Jy kan ook die radius van die sirkel en die booglengte na vind die sentrale hoek . Noem die maat van die sentrale hoek θ. Dan: θ = s ÷ r, waar s die booglengte is en r die radius.
Behalwe hierbo, hoe vind jy die sentrale hoek van 'n sektor? Bepaling van die sentrale hoek Van die Sektor Oppervlakte Met ander woorde: (πr2) × ( sentrale hoek in grade ÷ 360 grade) = sektor gebied. As die sentrale hoek word gemeet in radiale, die formule in plaas daarvan word: sektor oppervlakte = r2 × ( sentrale hoek in radiale ÷ 2).
Behalwe hierbo, wat is die oppervlakte van 'n sektor?
Die area van 'n sektor in terme van L kan verkry word deur die totaal te vermenigvuldig gebied πr2 deur die verhouding van L tot die totale omtrek 2πr.
Wat is die formule vir omtrek?
Om die omtrek van a te bereken sirkel , gebruik die formule C = πd, waar "C" die omtrek is, "d" die deursnee is en π 3,14 is. As jy die radius in plaas van die deursnee het, vermenigvuldig dit met 2 om die deursnee te kry. Jy kan ook die formule gebruik vir omtrek van a sirkel gebruik radius, wat C = 2πr is.
Aanbeveel:
Hoe vind jy die komponentvorm van 'n vektor gegewe die grootte en hoek?
VIDEO As dit in ag geneem word, is 0 'n eenheidsvektor? A eenheidsvektor is 'n vektor wat 'n grootte van 1 het. Die notasie verteenwoordig die norm, of grootte, van vektor v. Die basiese eenheidsvektore is ek = (1, 0 ) en j = ( 0 , 1) wat van lengte 1 is en rigtings langs die positiewe x-as en y-as onderskeidelik het.
Hoe vind jy die vergelyking van 'n lyn gegewe 'n punt en 'n parallelle lyn?
Die vergelyking van die lyn in die hellingafsnitvorm is y=2x+5. Die helling van die parallellyn is dieselfde: m=2. Dus, die vergelyking van die parallelle lyn is y=2x+a. Om 'n te vind, gebruik ons die feit dat die lyn deur die gegewe punt moet gaan:5=(2)⋅(−3)+a
Hoe vind jy 'n sentrale hoek?
Dus, die sentrale hoek is in wese die booglengte vermenigvuldig met 360, die grade van 'n volle sirkel, gedeel deur die omtrek van die sirkel. Soos jy kan sien, is die booglengte bloot die omtrek van 'n sirkel (2πR) vermenigvuldig met die verhouding van die booghoek tot die volle 360 hoek van 'n sirkel
Sal dit sin maak om die vergelyking van 'n lyn parallel aan 'n gegewe lyn en deur 'n punt op die gegewe lyn te vind?
Die vergelyking van 'n lyn wat parallel of loodreg op 'n gegewe lyn is? Moontlike antwoord: Die hellings van parallelle lyne is gelyk. Vervang die bekende helling en die koördinate van 'n punt op die ander lyn in die punt-helling vorm om die vergelyking van die parallelle lyn te vind
Hoe vind jy die hoek van 'n sektor in 'n sirkelgrafiek?
1 Antwoord In enige sektor is daar 3 dele wat oorweeg moet word: Die booglengte is 'n breukdeel van die omtrek. Hierdie sektorarea is 'n breukdeel van die hele oppervlakte. Hierdie sektorhoek is 'n breuk van 360° As die sektor 20% van die sirkelgrafiek is, is elkeen van hierdie dele 20% van die geheel. 20%×360° 20100×360=72°