Video: Kan chi-kwadraat negatief wees?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Doen jy bedoel: Kan waardes van chi vierkant ooit wees negatief ? Die antwoord is nee. Die waarde van a chi vierkant kan nie wees nie negatief want dit is gebaseer op 'n som van vierkantig verskille (tussen verkry en verwagte resultate).
Net so, hoekom is die chi-kwadraatverspreiding altyd positief?
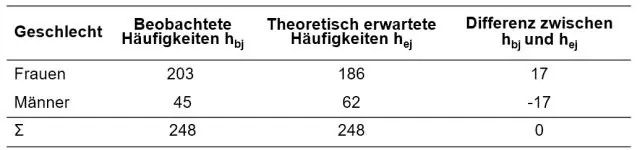
Die berekende waarde van Chi - Vierkantig is altyd positief want die verskil tussen die Waargenome frekwensie en die Verwagte frekwensie is vierkantig , dit is (O - E)2 en die demoninator is die getal wat verwag word wat ook moet wees positief . Die Chi - Vierkant verspreiding is positief skeef.
Behalwe hierbo, kan chi-kwadraat 0 wees? In statistiek, die nie-sentrale chi - vierkantig verspreiding met nul grade van vryheid kan gebruik word om die nulhipotese te toets dat 'n steekproef van 'n eenvormige verspreiding op die interval ( 0 , 1). Dit is onbenullig dat 'n "sentrale" chi -vierkant verspreiding met nul grade van vryheid konsentreer alle waarskynlikheid by nul.
Net so, kan jy 'n negatiewe T-waarde hê?
As dit kleiner is as die hipotese waarde , Dan die t -statistiek negatief sal wees . As dit groter is, sal die t -statistiek sal wees positief. A negatief teken impliseer dat die steekproefgemiddeld minder is as die veronderstelde gemiddelde.
Hoe verwerp jy die nulhipotese Chi Square?
Met ander woorde, wanneer die berekende x2 statistiek oorskry die kritieke waarde in die tabel vir 'n 0,05 waarskynlikheidsvlak, dan kan ons verwerp die nulhipotese van gelyke verdelings.
Aanbeveel:
Hoe lank na 'n aardbewing kan daar naskokke wees?
Tien dae ná die hoofskok is daar net 'n tiende van die aantal naskokke. 'n Aardbewing sal 'n naskok genoem word solank die tempo van aardbewings hoër is as wat dit voor die hoofskok was. Vir groot aardbewings kan dit vir dekades aanhou. Groter aardbewings het meer en groter naskokke
Kan daar 'n vulkaan in Los Angeles wees?
Daar is geen vulkane in Los Angeles nie. Die naaste vulkaniese aktiwiteit is die Lavic vulkaniese veld en Coso vulkaniese veld
Kan elastiese potensiële energie negatief wees?
Omdat jy werk aan die veer doen, d.w.s. energie daarheen oordra, verhoog jy die potensiële energie wat daarin gestoor word. Om die sinvolle definisie te maak dat die PE nul is wanneer x=0 die potensiële energie kan nooit negatief wees nie
Kan die som van 'n rekenkundige reeks negatief wees?
Die gedrag van die rekenkundige ry hang af van die gemeenskaplike verskil d. As die gemeenskaplike verskil, d, is: Positief, sal die ry vorder na oneindigheid (+∞) Negatief, sal die ry regresseer na negatiewe oneindigheid (−∞)
Hoekom negatief en negatief is positief?
Wanneer jy 'n negatief met 'n negatief vermenigvuldig, kry jy 'n positiewe, want die twee negatiewe tekens word uitgekanselleer