Video: Kan die som van 'n rekenkundige reeks negatief wees?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Die gedrag van die rekenkundige volgorde hang af van die gemeenskaplike verskil d. As die gemeenskaplike verskil, d, is: Positief, die volgorde sal vorder na oneindigheid (+∞) Negatief , die volgorde sal regressie na negatief oneindigheid (−∞)
Verder, kan die som van 'n reeks negatief wees?
Jy praat van die som van 'n oneindige reeks wat impliseer dat die reeks is meetkundig, aangesien 'n oneindige rekenkunde reeks kan nooit konvergeer nie. Let wel, die algemene verhouding moet |r| wees < 1 vir 'n som om te bestaan. Dus as die gemeenskaplike verhouding daar positief is kan wees nee negatiewe som.
Ook, wat is die som van eindige rekenkundige reekse? Die som van (n) terme van 'n rekenkundige reeks is (5{n}^{2}-11n) vir alle waardes van (n). Bepaal die gemeenskaplike verskil. Die som van 'n rekenkundige reeks is (ext{100}) keer sy eerste term, terwyl die laaste term (ext{9}) keer die eerste term is.
Hoe vind jy die som van 'n rekenkundige reeks daarvan?
Om vind die som van 'n rekenkunde ry, begin deur die eerste en laaste nommer in die ry te identifiseer. Tel dan daardie getalle bymekaar en deel die som met 2. Laastens, vermenigvuldig daardie getal met die totale aantal terme in die ry tot vind die som.
Wat is N in reeks?
Die eerste term is a1, die gemeenskaplike verskil is d, en die aantal terme is. Die som van 'n rekenkunde reeks word gevind deur die aantal terme maal die gemiddelde van die eerste en laaste terme te vermenigvuldig. Om te vind, gebruik die eksplisiete formule vir 'n rekenkunde volgorde . Ons los 3 + (– 1)·4 = 99 op om = 25 te kry.
Aanbeveel:
Kan chi-kwadraat negatief wees?
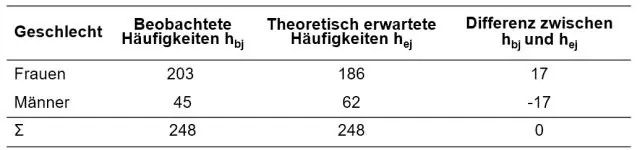
Bedoel jy: Kan waardes van chi-kwadraat ooit negatief wees? Die antwoord is nee. Die waarde van 'n chi-kwadraat kan nie negatief wees nie, want dit is gebaseer op 'n som van kwadraatverskille (tussen verkry en verwagte resultate)
Wat is die som van die rekenkundige reeks?
Die som van 'n rekenkundige reeks word gevind deur die aantal terme maal die gemiddelde van die eerste en laaste terme te vermenigvuldig. Voorbeeld: 3 + 7 + 11 + 15 + ··· + 99 het a1 = 3 en d = 4
Kan elastiese potensiële energie negatief wees?
Omdat jy werk aan die veer doen, d.w.s. energie daarheen oordra, verhoog jy die potensiële energie wat daarin gestoor word. Om die sinvolle definisie te maak dat die PE nul is wanneer x=0 die potensiële energie kan nooit negatief wees nie
Hoe vind jy die som van 'n eindige rekenkundige of meetkundige reeks?
Die formule vir die som van n terme van 'n meetkundige ry word gegee deur Sn = a[(r^n - 1)/(r - 1)], waar a die eerste term is, n die term getal is en r die term is algemene verhouding
Hoekom negatief en negatief is positief?
Wanneer jy 'n negatief met 'n negatief vermenigvuldig, kry jy 'n positiewe, want die twee negatiewe tekens word uitgekanselleer