INHOUDSOPGAWE:
Video: Hoe evalueer jy saamgestelde funksies?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Evaluering van saamgestelde funksies met behulp van grafieke
- Vind die gegewe insette na die binneste funksie op die x-as van sy grafiek.
- Lees die uitset van die binnekant af funksie vanaf die y-as van sy grafiek.
- Vind die binneste funksie uitset op die x-as van die grafiek van die buitenste funksie .
Hierin, hoe skryf en evalueer jy saamgestelde funksies?
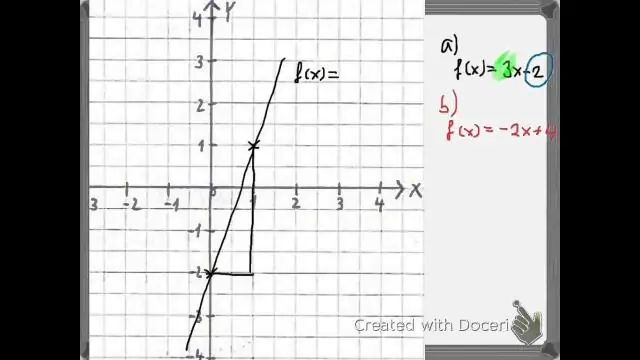
Om 'n saamgestelde funksie waar ons g(x) in die funksie f(x), ons kan skryf dit f(g(x)). Let daarop dat in plaas daarvan om bloot 'n x in die funksie , vervang ons die hele g(x) funksie . Wanneer ons dit doen, het ons f(g(x)) = (3x) + 2. Aan die linkerkant sal jy sien dat die g funksie is binne die f funksie.
Net so, wat is 'n saamgestelde funksie voorbeeld? A saamgestelde funksie is 'n funksie dit hang van 'n ander af funksie . A saamgestelde funksie word geskep wanneer een funksie word in 'n ander vervang funksie . Vir voorbeeld , f(g(x)) is die saamgestelde funksie wat gevorm word wanneer g(x) vir x in f(x) vervang word. In die samestelling (f ο g)(x), die domein van f word g(x).
Mense vra ook, wat is die stappe om 'n saamgestelde funksie op te los?
Hier is die stappe ons kan gebruik om die te vind samestelling van twee funksies : Stap 1: Herskryf die samestelling in 'n ander vorm. Byvoorbeeld, die samestelling (f g)(x) moet herskryf word as f(g(x)). Stap 2: Vervang elke voorkoms van x wat aan die buitekant gevind word funksie met die binnekant funksie.
Wat word bedoel met saamgestelde funksie?
: a funksie wie se waardes gevind word uit twee gegewe funksies deur een toe te pas funksie op 'n onafhanklike veranderlike en dan die tweede toe te pas funksie tot die resultaat en wie se domein bestaan uit daardie waardes van die onafhanklike veranderlike waarvoor die resultaat opgelewer deur die eerste funksie lê in die domein van die tweede.
Aanbeveel:
Hoe doen jy waarskynlikheid Saamgestelde gebeurtenisse?
Die bepaling van die waarskynlikheid van 'n saamgestelde gebeurtenis behels die vind van die som van die waarskynlikhede van die individuele gebeurtenisse en, indien nodig, die verwydering van enige oorvleuelende waarskynlikhede. 'n Eksklusiewe saamgestelde gebeurtenis is een waarin die veelvuldige gebeurtenisse nie oorvleuel nie. In wiskundige terme: P(C) = P(A) + P(B)
Hoe vermenigvuldig jy saamgestelde funksies?
Vermenigvuldiging en samestelling van funksies Om 'n funksie met 'n skalaar te vermenigvuldig, vermenigvuldig elke uitset met daardie skalaar. Wanneer ons f (g(x)) neem, neem ons g(x) as die invoer van die funksie f. Byvoorbeeld, as f (x) = 10x en g(x) = x + 1, dan vind ons f (g(4)), g(4) = 4 + 1 + 5, en evalueer dan f (5) ) = 10(5) = 50. Voorbeeld: f (x) = 2x - 2, g(x) = x2 - 8
Hoe kan 'n model help om die waarskynlikheid van 'n saamgestelde gebeurtenis te vind?
Definisie van Waarskynlikheid van Saamgestelde Gebeurtenisse 'n Saamgestelde gebeurtenis is een waarin daar meer as een moontlike uitkoms is. Die bepaling van die waarskynlikheid van 'n saamgestelde gebeurtenis behels die vind van die som van die waarskynlikhede van die individuele gebeurtenisse en, indien nodig, die verwydering van enige oorvleuelende waarskynlikhede
Waarom word trigonometriese funksies sirkelvormige funksies genoem?
Trigonometriese funksies word soms sirkelvormige funksies genoem. Dit is omdat die twee fundamentele trigonometriese funksies – die sinus en die cosinus – gedefinieer word as die koördinate van 'n punt P wat rondbeweeg op die eenheidsirkel van radius 1. Die sinus en die cosinus herhaal hul uitsette met gereelde intervalle
Wat is die korrekte volgorde om algebraïese uitdrukkings te evalueer?
Vir wiskunde om te werk is daar net een volgorde van bewerkings om 'n wiskundige uitdrukking te evalueer. Die volgorde van bewerkings is Hakies, Eksponente, Vermenigvuldiging en deling (van links na regs), Optel en Aftrekking (van links na regs)