INHOUDSOPGAWE:
Video: Hoe vermenigvuldig jy saamgestelde funksies?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Vermenigvuldiging en samestelling van funksies
- Om vermenigvuldig a funksie deur 'n skalaar, vermenigvuldig elke uitset volgens daardie skalaar.
- Wanneer ons f (g(x)) neem, neem ons g(x) as die inset van die funksie f.
- Byvoorbeeld, as f (x) = 10x en g(x) = x + 1, dan vind ons f (g(4)), g(4) = 4 + 1 + 5, en evalueer dan f (5)) = 10(5) = 50.
- Voorbeeld: f (x) = 2x - 2, g(x) = x2 - 8.
Gevolglik, hoe doen jy veelvuldige funksies?
Vermenigvuldiging van Funksies Om vermenigvuldig a funksie deur 'n ander funksie , vermenigvuldig hul uitsette. Byvoorbeeld, as f (x) = 2x en g(x) = x + 1, dan is fg(3) = f (3)×g(3) = 6×4 = 24. fg(x) = 2x(x) + 1) = 2x2 + x.
Daarbenewens, hoe teken jy 'n funksie? Oorweeg die funksie f(x) = 2 x + 1. Ons herken die vergelyking y = 2 x + 1 as die Helling-afsnit-vorm van die vergelyking van 'n lyn met helling 2 en y-afsnit (0, 1). Dink aan 'n punt wat op die beweeg grafiek van f. Soos die punt na regs beweeg, styg dit.
Vervolgens kan mens ook vra, wat is die produk van twee funksies?
Wanneer jy vermenigvuldig twee funksies saam, sal jy 'n derde kry funksie as gevolg daarvan, en daardie derde funksie sal die wees produk van die twee oorspronklike funksies . Byvoorbeeld, as jy f(x) en g(x) vermenigvuldig, sal hulle produk sal h(x)=fg(x), of h(x)=f(x)g(x) wees. Jy kan ook die evalueer produk op 'n bepaalde punt.
Hoe los jy 'n funksie op?
Vir funksies , beteken die twee notasies presies dieselfde ding, maar "f (x)" gee jou meer buigsaamheid en meer inligting. Jy het vroeër gesê "y = 2x + 3; oplos vir y wanneer x = –1". Nou sê jy "f (x) = 2x + 3; vind f (–1)" (uitgespreek as "f-van-x is gelyk aan 2x plus drie; vind f-van-negatief-een").
Aanbeveel:
Hoe evalueer jy saamgestelde funksies?
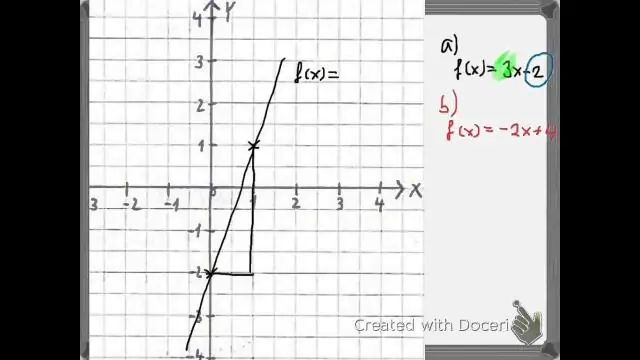
Evaluering van saamgestelde funksies met behulp van grafieke Vind die gegewe invoer na die binneste funksie op die x-as van sy grafiek. Lees die uitset van die binneste funksie vanaf die y-as van sy grafiek af. Vind die binne-funksie-uitset op die x-as van die grafiek van die buitenste funksie
Hoe vermenigvuldig jy verskillende vierkantswortels?
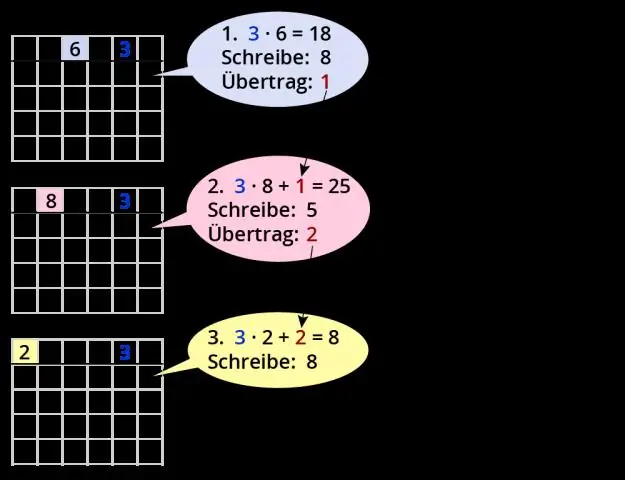
Metode 2 Vermenigvuldig vierkantswortels met koëffisiënte Vermenigvuldig die koëffisiënte. 'n Koëffisiënt is 'n getal voor die radikale teken. Vermenigvuldig die radikaande. Faktoreer enige perfekte blokkies in die radicand, indien moontlik. Vermenigvuldig die vierkantswortel van die volmaakte vierkant met die koëffisiënt
Hoe kruis jy vermenigvuldig en vergelyk breuke?
Om twee breuke te kruisvermenigvuldig: Vermenigvuldig die teller van die eerste breuk met die noemer van die tweede breuk en skryf die antwoord neer. Vermenigvuldig die teller van die tweede breuk met die noemer van die eerste breuk en skryf die antwoord neer
Waarom word trigonometriese funksies sirkelvormige funksies genoem?
Trigonometriese funksies word soms sirkelvormige funksies genoem. Dit is omdat die twee fundamentele trigonometriese funksies – die sinus en die cosinus – gedefinieer word as die koördinate van 'n punt P wat rondbeweeg op die eenheidsirkel van radius 1. Die sinus en die cosinus herhaal hul uitsette met gereelde intervalle
Hoe vermenigvuldig jy rasionale funksies?
Q en S is nie gelyk aan 0 nie. Stap 1: Faktoreer beide die teller en die noemer. Stap 2: Skryf as een breuk. Stap 3: Vereenvoudig die rasionele uitdrukking. Stap 4: Vermenigvuldig enige oorblywende faktore in die teller en/of noemer. Stap 1: Faktoreer beide die teller en die noemer. Stap 2: Skryf as een breuk