INHOUDSOPGAWE:
Video: Hoe los jy x 2-vergelykings op?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Metode 2 Gebruik die Kwadratiese Formule
- Kombineer al die soortgelyke terme en skuif hulle na die een kant van die vergelyking .
- Skryf neer die kwadratiese formule .
- Identifiseer die waardes van a, b en c in die kwadratiese vergelyking .
- Vervang die waardes van a, b en c in die vergelyking .
- Doen die wiskunde.
- Vereenvoudig die vierkantswortel.
Verder, hoe los jy vir x in 'n vergelyking op?
Om los op vir x wanneer die vergelyking sluit 'n eksponent in, begin deur die term met die eksponent te isoleer. Isoleer dan die veranderlike met die eksponent deur beide kante te deel deur die koëffisiënt van die x term om jou antwoord te kry. As die vergelyking breuke het, begin deur die breuke te kruisvermenigvuldig.
Tweedens, wat is die oplossings vir die vergelyking? An vergelyking is 'n algebraïese uitdrukking wat tipies onbekende veranderlikes met ander veranderlikes of konstante in verband bring. Byvoorbeeld, x + 2 = 15 is an vergelyking , as isy2 = 4. Die oplossing , of wortel, van 'n vergelyking is enige waarde of stel waardes wat in die vergelyking om dit 'n ware verklaring te maak.
Verder, hoe los jy vir x in 'n kwadratiese vergelyking op?
Los op vir x : 2 x 2 + 3 x + 2 = 0. Omdat a ≠ 1, vermenigvuldig deur die vergelyking deur. Daar is geen oplossing in die reële getallestelsel nie. Dit kan jou interesseer om te weet dat die voltooiing van die vierkant proses vir kwadratiese vergelykings op te los is gebruik op die vergelyking byl2 + bx + c = 0 om die af te lei kwadraties formule.
Hoe los jy x- en y-afsnitte op?
Om die x - onderskep van 'n gegewe lineêre vergelyking , prop in 0 vir ' y 'en los op vir 'x '. Om die y - onderskep , prop 0 in vir ' x 'en oplos vir ' y '. In hierdie tutoriaal sal jy sien hoe om die x - onderskep en die y - onderskep vir 'n gegewe lineêre vergelyking . Kyk daarna!
Aanbeveel:
Hoe los jy 'n kwadratiese vergelyking op deur die nulfaktorwet te gebruik?
Hieruit kan ons aflei dat: As die produk van enige twee getalle nul is, dan is een of albei van die getalle nul. Dit wil sê, as ab = 0, dan is a = 0 of b = 0 (wat die moontlikheid insluit dat a = b = 0). Dit word die nulfaktorwet genoem; en ons gebruik dit dikwels om kwadratiese vergelykings op te los
Hoe maak jy 'n remklauwsuier los?
Om 'n remklauwsuier wat vasgeval het te verwyder, kan die hidrouliese druk van die remstelsel self gebruik word. Verwyder die kaliper van die skyf en pomp die rempedaal om die suier verby die geroeste gedeelte te beweeg. Nou behoort jy dit te kan demonteer en herbou
Hoe los jy Hardy Weinberg-probleme op?
VIDEO Behalwe dit, hoe vind jy P en Q in Hardy Weinberg? Sedert bl = 1 - q en q bekend is, is dit moontlik om bereken bl ook. Weet p en q , Dit is 'n eenvoudige saak om hierdie waardes in die Hardy - Weinberg vergelyking (p² + 2pq + q² = 1).
Hoe los jy ideale gaswet op?
Ideale Gas Wet Formule Ideale Gas Wet Formule Vrae: Antwoord: Die Volume is V = 890.0mL en die Temperatuur is T = 21°C en die Druk is P = 750mmHg. PV = nRT. Antwoord: Die aantal mol is n = 3.00mol, temperatuur is T = 24°C en druk is P = 762.4 mmHg. PV = nRT
Hoe los jy vermenigvuldiging en deling van breuke op?
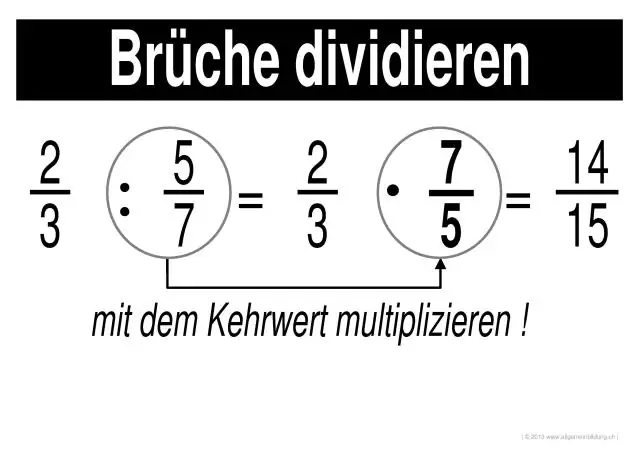
Vermenigvuldig en deel breuke Stap 1: Vermenigvuldig die tellers van elke breuk met mekaar (die getalle bo). Die resultaat is die teller van die antwoord. Stap 2: Vermenigvuldig die noemers van elke breuk met mekaar (die getalle aan die onderkant). Die resultaat is die noemer van die antwoord. Stap 3: Vereenvoudig of verklein die antwoord