Video: Hoekom is die derdemagswortel van 'n negatiewe getal 'n negatiewe getal?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
A negatiewe getal se derdemagswortel sal altyd wees negatief
Sedert cubing a nommer beteken om dit te verhoog tot die 3de mag-wat vreemd-die is kubuswortels van negatiewe getalle moet ook wees negatief . Wanneer die skakelaar af is (blou), is die resultaat negatief . Wanneer die skakelaar aan is (geel), is die resultaat positief.
Net so word gevra, hoekom kan jy die derdemagswortel van 'n negatiewe getal neem?
Die rede dat ons kan het nie die vierkant (of kwartier nie) wortel van 'n negatiewe getal is dat twee negatiewe altyd kanselleer om 'n pluspunt te gee; dus die vierkant wortel van 'n negatiewe getal ongedefinieerd is. Die regte kubuswortel van enige negatief Werklike nommer is negatief.
Behalwe hierbo, wat is die wortel van 'n negatiewe getal? Die vierkant wortel van 'n nommer y word gedefinieer as die waarde x sodanig dat x2=y. Egter vir enige werklike nommer x, x2≧0. Wanneer ons sê dat die vierkant wortel van 'n negatiewe getal "bestaan nie", bedoel ons dat daar geen werklike is nie nommer oplossing. As ons egter kompleks oorweeg getalle , kry ons dan 'n oplossing vir √−1=i.
Behalwe hierbo, is kubuswortels altyd positief?
Dit is een area waar 'n vierkant gevind word wortel en vind a kubuswortel verskil. Kubuswortels (en enige ander vreemde wortels ) is nie gemoeid met negatiewe waardes onder die radikale nie, want perfek blokkies negatief kan wees. Volmaakte vierkante (en enige ander selfs volmaakte kragte) kan nie negatief wees nie. terwyl selfs wortels is altyd positief.
Hoekom is 'n negatiewe getal kwadraat steeds negatief?
Ja, jy kan a vierkantig maak negatiewe getal . Dit is omdat om a te vier nommer beteken net om dit met homself te vermenigvuldig. Byvoorbeeld, (-2) vierkantig is (-2)(-2) = 4. Let daarop dat dit positief is, want wanneer jy twee vermenigvuldig negatiewe getalle jy kry 'n positiewe resultaat.
Aanbeveel:
Wat is die derdemagswortel van 40 in radikale vorm?
Die faktor van 40 waarvan ons die derdemagswortel kan neem, is 8. Ons kan 40 skryf as (8)(5) en dan die produkreël van radikale gebruik om die 2 getalle te skei. Ons kan die derdemagswortel van 8 neem, wat 2 is, maar ons sal die 5 onder die derdemagswortel moet laat
Wat is die omgekeerde van die kubering van 'n getal?
Neem x, kubus om x3 te kry en deel deur 8 om x3/8 te kry. Hierdiex3/8 word die inverse funksie genoem en word geskryf as f-1(x)
Hoekom is die EMK nul wanneer die spoel deur die presiese middelpunt van die magneet beweeg?
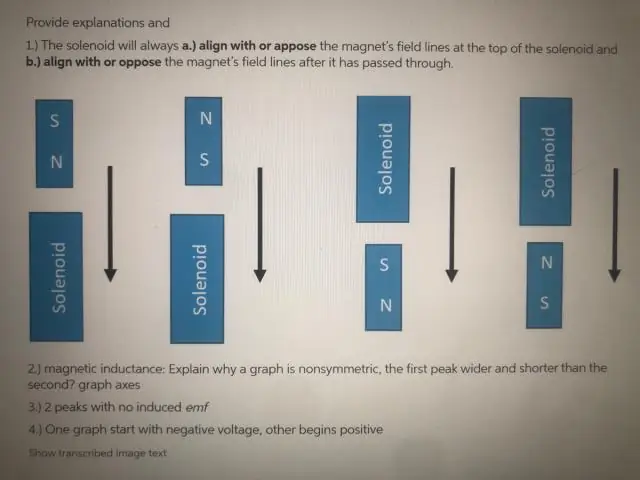
Die emk is net nul vir 'n oomblik as die magneet deur die presiese middelpunt van die spoel beweeg. Dit is omdat die effek van die N-pool aan die een kant van die magneet op daardie kant van die spoel presies uitgekanselleer word deur die effek van die S-pool van die magneet aan die ander kant van die spoel
Is negatiewe 8 'n irrasionale getal?
Antwoord en verduideliking: Negatiewe 8, wat ook as -8 geskryf kan word, is 'n rasionale getal. 'n Rasionale getal is per definisie die kwosiënt wat ontstaan wanneer een heelgetal is
Kan jy 'n derdemagswortel met 'n vierkantswortel vermenigvuldig?
Die produk wat tot 'n magsreël verhef word, is belangrik omdat jy dit kan gebruik om radikale uitdrukkings te vermenigvuldig. Let daarop dat die wortels dieselfde is-jy kan byvoorbeeld vierkantswortels met vierkantswortels, of derdemagswortels met derdemagswortels kombineer. Maar jy kan nie 'n vierkantswortel en 'n derdemagswortel met hierdie reël vermenigvuldig nie