Video: Is p2 'n subruimte van p3?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Ja! Aangesien elke polinoom van graad tot 2 ook 'n polinoom van graad tot 3 is, P2 is 'n subset van P3 . En ons weet dit reeds P2 is 'n vektorruimte, dus is dit 'n subruimte van P3 . Dit wil sê, R2 is nie 'n subset van R3 nie.
Mense vra ook, is die versameling van alle polinome van graad 3 'n subruimte van p3?
1. P3 (F) is die vektorruimte van alle polinome van graad ≦ 3 en met koëffisiënte in F. Die dimensie is 2 omdat 1 en x lineêr onafhanklik is polinome wat oor die subruimte , en daarom is hulle 'n basis hiervoor subruimte . (b) Laat U die subset van P3 (F) bestaande uit alle polinome van graad 3.
wat is 'n subruimte van r3? Streng gesproke, A Subruimte is 'n vektorruimte wat by 'n ander groter vektorruimte ingesluit is. Daarom geld alle eienskappe van 'n vektorruimte, soos om gesluit te wees onder optelling en skalêre vermenigvuldiging steeds wanneer dit toegepas word op die Subruimte . bv. Ons weet almal R3 is 'n vektorruimte.
Mense vra ook, wat is p2 in lineêre algebra?
Laat P2 wees die ruimte van polinome van hoogstens 2, en definieer die lineêr transformasie T: P2 → R2 T(p(x)) = [p(0) p(1)] Byvoorbeeld T(x2 + 1) = [1 2].
Wat is die nul polinoom?
Nul polinoom . Die konstante polinoom . wie se koëffisiënte almal gelyk is aan 0. Die ooreenstemmende polinoom funksie is die konstante funksie met waarde 0, ook genoem die nul kaart. Die nul polinoom is die toevoeging identiteit van die toevoeging groep van polinome.
Aanbeveel:
Hoe verskil die vorm van 'n plantsel van dié van 'n diersel?
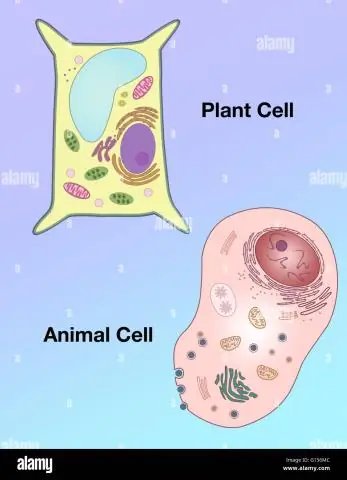
Vakuole: Plantselle het 'n groot vakuole, terwyl dierselle veelvuldige klein vakuole bevat. Vorm: Plantselle het 'n meer reëlmatige vorm (gewoonlik reghoekig), terwyl dierselle onreëlmatige vorms het. Lysosome: is oor die algemeen teenwoordig in dierselle, terwyl hulle afwesig is in plantselle
Hoe is die wet van behoud van energie van toepassing op energietransformasies?
Die wet van behoud van energie bepaal dat energie nie geskep of vernietig kan word nie - slegs van een vorm van energie na 'n ander omgeskakel kan word. Dit beteken dat 'n stelsel altyd dieselfde hoeveelheid energie het, tensy dit van buite af bygevoeg word. Die enigste manier om energie te gebruik, is om energie van een vorm na 'n ander te transformeer
Hoe vind jy die subruimte?
VIDEO Is ook 'n basis van die subruimte? Ons het voorheen 'n gedefinieer basis vir 'n subruimte as 'n minimum stel vektore wat oor die subruimte . Daardie is, 'n basis vir 'n k-dimensionele subruimte is 'n stel k vektore wat oor die subruimte .
Hoe verskil 'n kristal van aluin van 'n kristal van kaliumaluminiumsulfaat?
A) Antwoord is: kaliumaluminiumsulfaat is kristal met kubieke struktuur, kaliumaluminiumsulfaat dodekahidraat (aluin) is hidraat (bevat water of sy samestellende elemente)
Hoe bewys jy 'n matriks is 'n subruimte?
Die Sentraliseerder van 'n Matriks is 'n Subruimte Laat V die vektorruimte van n×n matrikse wees, en M∈V 'n vaste matriks. Definieer W={A∈V∣AM=MA}. Die versameling W word hier die sentraliseerder van M in V genoem. Bewys dat W 'n subruimte van V is