Video: Hoe weet jy of 'n transformasie een tot een is?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Wanneer 'n lineêre transformasie word beskryf in terme van 'n matriks is dit maklik om bepaal of die lineêre transformasie is een-tot-een of nie deur die lineêre afhanklikheid van die kolomme van die matriks na te gaan nie. As die kolomme is lineêr onafhanklik, die lineêre transformasie is een-tot-een.
Wat beteken dit in hierdie verband as 'n lineêre transformasie een tot een is?
Een-tot-een lineêre transformasies . Definisie : A lineêre transformasie wat afsonderlike punte/vektore van in afsonderlike punte/vektore in kaart, word gesê dat dit 'n een-tot-een transformasie of 'n inspuiting transformasie . Dus vir elke vektor bestaan daar presies een vektor sodanig dat.
Mens kan ook vra, kan 'n lineêre transformasie op maar nie een tot een wees nie? In matriks terme beteken dit dat a transformasie met matriks A is op as Ax=b 'n oplossing het vir enige b in die reeks. As 'n transformasie is op maar nie een-tot-een nie , jy kan dink aan die domein dat dit te veel vektore het om in die reeks te pas.
Hiervan, kan 'n matriks een tot een wees en nie op nie?
In die besonder, die enigste matrikse daardie kan wees albei een tot een en op vierkantig is matrikse . Aan die ander kant, jy kan het an m×n matriks met m<n dit is op , of een dit wil sê nie op nie . En jy kan het m×n matrikse met m>n wat is een tot een , en matrikse dit is nie een-tot-een nie.
Hoe bewys jy 'n lineêre transformasie?
Vir elke y ∈ Y is daar ten minste een x ∈ X met f(x) = y. Elke element van die kodomein van f is 'n uitset vir een of ander inset. Ons kan vasstel of a lineêre transformasie is een-tot-een of op deur die kolomme van sy standaardmatriks te inspekteer (en ryvermindering).
Aanbeveel:
Hoe weet jy of 'n transformasie 'n dilatasie is?
'n Beskrywing van 'n dilatasie sluit die skaalfaktor (of verhouding) en die middelpunt van die dilatasie in. Die middelpunt van dilatasie is 'n vaste punt in die vlak. As die skaalfaktor groter as 1 is, is die beeld 'n vergroting ('n rek). As die skaalfaktor tussen 0 en 1 is, is die beeld 'n verkleining ('n krimp)
Hoe beskryf jy transformasie in bakterieë?
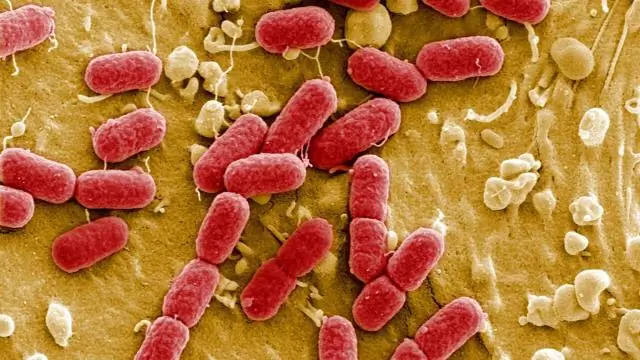
Die stukkie DNS of geen van belang word uit sy oorspronklike DNS-bron gesny deur 'n beperkingsensiem te gebruik en dan in die plasmied geplak deur ligasie. Die plasmied wat die vreemde DNA bevat, is nou gereed om in bakterieë ingevoeg te word. Hierdie proses word transformasie genoem
Hoe kan u transformasie in 'n sin gebruik?
Transformeer sinsvoorbeelde Ons kon in duisende jare nog nooit 'n vamp in 'n mens omskep nie. Wesley het geglo dat die genade van God elke lewe wat dit ontvang kon transformeer. Haar beleid was tot onlangs om hulle in Franse grondgebied te omskep
Hoe het Avery en sy groep bepaal watter molekule die belangrikste vir transformasie was?
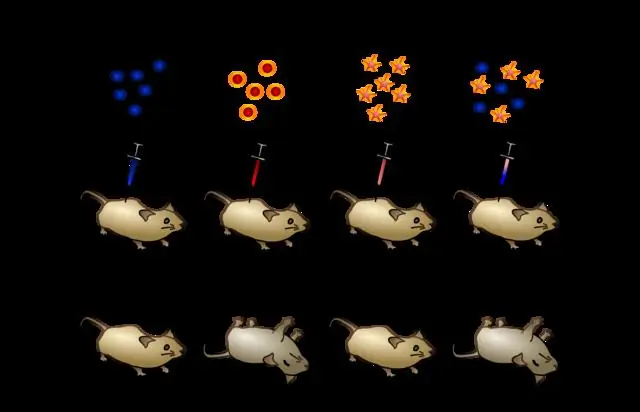
Beskryf kortliks hoe Avery en sy groep bepaal het watter molekule die belangrikste vir transformasie was. Avery en sy groep het twee verskillende ensieme gebruik op 'n uittreksel van hitte-gedood bakterieë. Die een het DNA vernietig, die ander het alles behalwe. Hulle het gevind dat transformasie steeds plaasgevind het toe DNA teenwoordig was
Hoe word meganiese energie tydens oordrag of transformasie bewaar?
Die wet van behoud van energie bepaal dat vir enige sisteem, energie nie geskep of vernietig kan word nie; dit kan net van een vorm na 'n ander verander of van een voorwerp na 'n ander oordra. Meganiese energie kom in twee vorme voor: potensiële energie, wat gestoor energie is, en kinetiese energie, wat energie van beweging is