Hoe vind jy die simboliese voorstelling van 'n kwadratiese funksie?

Video: Hoe vind jy die simboliese voorstelling van 'n kwadratiese funksie?

2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33

Kwadratiese funksies kan simbolies voorgestel word deur die vergelyking , y(x) = byl² + bx + c, waar a, b en c konstantes is, en a ≠ 0. Daar word na hierdie vorm verwys as standaardvorm.

Mense vra ook, wat is die simboliese voorstelling van 'n funksie?

Funksies . Jy is waarskynlik die meeste vertroud met die simboliese voorstelling van funksies , soos die vergelyking, y = f(x). Funksies kan deur tabelle voorgestel word, simbole , of grafieke.

Net so, hoe bepaal jy die vorm van 'n kwadratiese grafiek? Vorm van die parabool

As a>0, dan het die parabool 'n minimum punt en dit maak opwaarts oop (U-vormig) bv.
As a<0, dan het die parabool 'n maksimum punt en dit open afwaarts (n-vormig) bv.
(a) Kontroleer of a>0 of a<0 om te besluit of dit U-vormig of n-vormig is.
(c) Die koördinate van die y-afsnit (vervang x=0).

Gevolglik, hoe stel jy 'n kwadratiese funksie voor?

Grafieke. A kwadratiese funksie is een van die vorm f(x) = ax² + bx + c, waar a, b en c getalle is met a nie gelyk aan nul nie. Die grafiek van a kwadratiese funksie is 'n kromme wat 'n parabool genoem word. Parabole kan opwaarts of afwaarts oopmaak en wissel in "breedte" of "steilheid", maar hulle het almal dieselfde basiese "U"-vorm.

Hoe los jy 'n funksie op?

Vir funksies , die twee notasies beteken presies dieselfde ding, maar "f (x)" gee jou meer buigsaamheid en meer inligting. Jy het vroeër gesê "y = 2x + 3; oplos vir y wanneer x = –1". Nou sê jy "f (x) = 2x + 3; vind f (–1)" (uitgespreek as "f-van-x is gelyk aan 2x plus drie; vind f-van-negatief-een").

Aanbeveel:

Wat is die vergelyking van kwadratiese funksie?

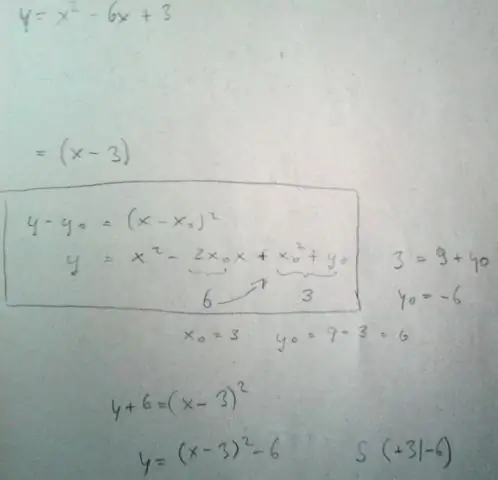
'n Kwadratiese funksie is een van die vorm f(x) = ax2 + bx + c, waar a, b en c getalle is met a nie gelyk aan nul nie. Die grafiek van 'n kwadratiese funksie is 'n kromme wat 'n parabool genoem word. Parabole kan opwaarts of afwaarts oopmaak en wissel in 'breedte' of 'steilheid', maar hulle het almal dieselfde basiese 'U'-vorm

Hoe vind jy 'n in 'n kwadratiese funksie?

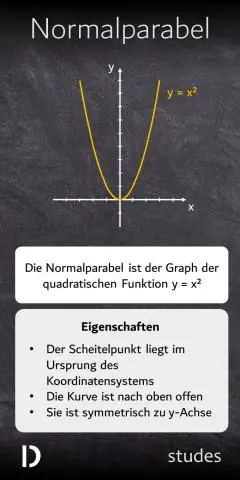
Daar word gesê dat die kwadratiese funksie f(x) = a(x -h)2 + k, a nie gelyk aan nul nie, in standaardvorm is. As a positief is, maak die grafiek opwaarts oop, en as a negatief is, maak dit afwaarts oop. Die simmetrielyn is die vertikale lyn x = h, en die hoekpunt is die punt (h,k)