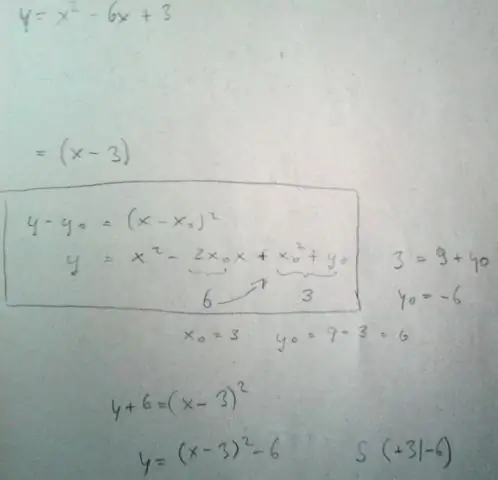
- Outeur Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:33.
- Laas verander 2025-06-01 05:03.
A kwadratiese funksie is een van die vorm f(x) = ax2 + bx + c, waar a, b en c getalle is met a nie gelyk aan nul nie. Die grafiek van a kwadratiese funksie is 'n kromme wat 'n parabool genoem word. Parabole kan opwaarts of afwaarts oopmaak en wissel in "breedte" of "steilheid", maar hulle het almal dieselfde basiese "U"-vorm.
Hiervan, WAT IS A in hoekpuntvorm?
y = a(x - h)2 + k, waar (h, k) die hoekpunt . Die "a" in die hoekpunt vorm is dieselfde "a" as. in y = byl2 + bx + c (dit wil sê, albei a's het presies dieselfde waarde). Die teken op "a" sê vir jou of die kwadratiese op of af oopmaak.
hoe bepaal jy 'n vergelyking is 'n funksie? Dit is relatief maklik om bepaal of 'n vergelyking is 'n funksie deur op te los vir y. Wanneer jy 'n vergelyking en 'n spesifieke waarde vir x, moet daar net een ooreenstemmende y-waarde vir daardie x-waarde wees. Byvoorbeeld, y = x + 1 is a funksie want y sal altyd een groter as x wees.
Op hierdie manier, hoe skryf jy 'n vergelyking vir 'n parabool?
Vir parabole wat sywaarts oopmaak, die standaardvorm vergelyking is (y - k)^2 = 4p(x - h). Die hoekpunt of punt van ons parabool word gegee deur die punt (h, k). Vir parabole wat op en af oopmaak, word die fokuspunt gegee deur (h, k + p). Vir parabole wat sywaarts oopmaak, die fokuspunt is (h + p, k).
Wat is die standaardvorm van 'n kwadratiese funksie?
A kwadratiese funksie is 'n funksie van graad twee. Die grafiek van a kwadratiese funksie is 'n parabool . Die generaal vorm van 'n kwadratiese funksie is f(x)=ax2+bx+c waar a, b en c reële getalle is en a≠0. Die standaardvorm van 'n kwadratiese funksie is f(x)=a(x−h)2+k.
Aanbeveel:
Hoe lyk die grafiek van 'n kwadratiese vergelyking?

Die grafiek van 'n kwadratiese funksie is 'n U-vormige kromme wat 'n parabool genoem word. Dit kan geteken word deur oplossings vir die vergelyking te teken, deur die hoekpunt te vind en die simmetrie-as te gebruik om geselekteerde punte te stip, of deur die wortels en hoekpunt te vind. Die standaardvorm van 'n kwadratiese vergelyking is
Hoe vind jy die simboliese voorstelling van 'n kwadratiese funksie?

Kwadratiese funksies kan simbolies voorgestel word deur die vergelyking, y(x) = ax2 + bx + c, waar a, b en c konstantes is, en a ≠ 0. Daar word na hierdie vorm verwys as standaardvorm
Hoe skakel jy 'n kwadratiese vergelyking van hoekpuntvorm na sakrekenaar om?

Sakrekenaar vir die omskakeling van die basiese vorm na die hoekpuntvorm y=x2+3x+5. x2+3x+5= || +(p2)2-(p2)2=0. || a2+2ab+b2=(a+b)2. || -1⋅-1=+1. xS=-32=-1.5. yS=-(32)2+5=2.75
Hoe vind jy die maksimum waarde van 'n kwadratiese funksie?

As jy die formule y = ax2 + bx + c kry, kan jy die maksimum waarde vind deur die formule max =c- (b2 / 4a) te gebruik. As jy die vergelyking y = a(x-h)2 + k het en teaterm is negatief, dan is die maksimum waarde k
Wat is die B in die kwadratiese vergelyking?

Kwadratiese funksie: Die kwadratiese funksie is f(x) = a * x^2 + b * x + c, wat jou vertel hoe die funksie in 'n grafiek sal lyk. B-waarde: Die b-waarde is die middelste getal, wat die getal langs en vermenigvuldig met die x is; 'n verandering in die waarde van b beïnvloed die parabool en die gevolglike grafiek
