Video: Hoe lyk die grafiek van 'n kwadratiese vergelyking?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Die grafiek van 'n kwadratiese funksie is 'n U- gevorm kromme wat 'n parabool genoem word. Dit Kan wees geteken deur oplossings te teken vir die vergelyking , deur die hoekpunt te vind en die simmetrie-as te gebruik om geselekteerde punte te plot, of deur die wortels en hoekpunt te vind. Die standaardvorm van 'n kwadratiese vergelyking is.
Wat dit betref, hoe lyk die grafiek van 'n kwadratiese?
Die grafiek van 'n kwadratiese funksie is 'n U- gevorm kromme wat 'n parabool genoem word. Die teken op die koëffisiënt a van die kwadraties funksie beïnvloed of die grafiek maak op of af oop. Die x-afsnitte is die punte waar die parabool die x-as kruis.
Tweedens, wat is K in standaardvorm? f (x) = a(x - h)2 + k , waar (h, k ) is die hoekpunt van die parabool. FYI: Verskillende handboeke het verskillende interpretasies van die verwysing " standaard vorm " van 'n kwadratiese funksie. (h, k ) is die hoekpunt van die parabool, en x = h is die simmetrie-as.
Hoe weet jy daarvan of 'n grafiek kwadraties is?
As die verskil is konstant, die grafiek lineêr is. As die verskil is nie konstant nie maar die tweede stel verskille is konstant, die grafiek is kwadraties . As die verskille volg 'n patroon soortgelyk aan die y-waardes, die grafiek eksponensieel is. Sien die voorbeelde hieronder vir duidelikheid.
Wat is die vorm van 'n parabool?
In wiskunde, a parabool is 'n vlakkromme wat spieëlsimmetries is en ongeveer U-vormig is.
Aanbeveel:
Hoe los jy 'n kwadratiese vergelyking op deur die nulfaktorwet te gebruik?
Hieruit kan ons aflei dat: As die produk van enige twee getalle nul is, dan is een of albei van die getalle nul. Dit wil sê, as ab = 0, dan is a = 0 of b = 0 (wat die moontlikheid insluit dat a = b = 0). Dit word die nulfaktorwet genoem; en ons gebruik dit dikwels om kwadratiese vergelykings op te los
Wat is die vergelyking van kwadratiese funksie?
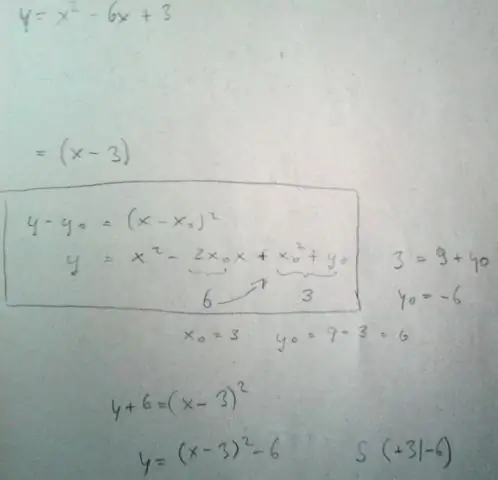
'n Kwadratiese funksie is een van die vorm f(x) = ax2 + bx + c, waar a, b en c getalle is met a nie gelyk aan nul nie. Die grafiek van 'n kwadratiese funksie is 'n kromme wat 'n parabool genoem word. Parabole kan opwaarts of afwaarts oopmaak en wissel in 'breedte' of 'steilheid', maar hulle het almal dieselfde basiese 'U'-vorm
Hoe skakel jy 'n kwadratiese vergelyking van hoekpuntvorm na sakrekenaar om?
Sakrekenaar vir die omskakeling van die basiese vorm na die hoekpuntvorm y=x2+3x+5. x2+3x+5= || +(p2)2-(p2)2=0. || a2+2ab+b2=(a+b)2. || -1⋅-1=+1. xS=-32=-1.5. yS=-(32)2+5=2.75
Wat is die B in die kwadratiese vergelyking?
Kwadratiese funksie: Die kwadratiese funksie is f(x) = a * x^2 + b * x + c, wat jou vertel hoe die funksie in 'n grafiek sal lyk. B-waarde: Die b-waarde is die middelste getal, wat die getal langs en vermenigvuldig met die x is; 'n verandering in die waarde van b beïnvloed die parabool en die gevolglike grafiek
Hoe skakel jy 'n kwadratiese vergelyking om van algemene vorm na standaardvorm?
Enige kwadratiese funksie kan in die standaardvorm f(x) = a(x - h) 2 + k geskryf word waar h en k gegee word in terme van koëffisiënte a, b en c. Kom ons begin met die kwadratiese funksie in algemene vorm en voltooi die vierkant om dit in standaardvorm te herskryf