INHOUDSOPGAWE:
Video: Hoe skakel jy 'n kwadratiese vergelyking van hoekpuntvorm na sakrekenaar om?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Sakrekenaar vir die omskakeling van die basiese vorm na die hoekpuntvorm
- y=x2+3x+5.
- x2+3x+5=
- || +(p2)2-(p2)2=0.
- || a2+2ab+b2=(a+b)2.
- || -1⋅-1=+1.
- xS=-32=-1.5.
- yS=-(32)2+5=2.75.
Dan, hoe skakel jy 'n kwadratiese vergelyking om na hoekpuntvorm?
Om omskep a kwadraties van y = byl2 + bx + c vorm aan hoekpunt vorm , y = a(x - h)2+ k, jy gebruik die proses om die vierkant te voltooi. Kom ons kyk na 'n voorbeeld. Skakel om y = 2x2 - 4x + 5 in hoekpunt vorm , en meld die hoekpunt . Vergelyking in y = ax2 + bx + c vorm.
Behalwe hierbo, wat is gefaktoriseerde vorm? A gefaktoriseerde vorm is 'n algebraïese uitdrukking tussen hakies. In werklikheid a gefaktoriseerde vorm is 'n produk van somme van produkte … of 'n som van produkte van somme … Enige logiese funksie kan voorgestel word deur 'n gefaktoriseerde vorm , en enige gefaktoriseerde vorm is 'n voorstelling van een of ander logiese funksie.
In hierdie verband, wat is die vergelyking om die hoekpunt te vind?
Parabole het altyd 'n laagste punt (of 'n hoogste punt, as die parabool onderstebo is). Hierdie punt, waar die parabool van rigting verander, word die " hoekpunt ". As die kwadratiese in die vorm geskryf word y = a(x – h)2 + k, dan die hoekpunt is die punt (h, k).
Wat is die hoekpunt van 'n parabool?
Die Toppunt van 'n Parabool . Die hoekpunt van 'n parabool is die punt waar die parabool kruis sy simmetrie-as. As die koëffisiënt van die x2 term positief is, die hoekpunt sal die laagste punt op die grafiek wees, die punt onderaan die " U "-vorm.
Aanbeveel:
Hoe los jy 'n kwadratiese vergelyking op deur die nulfaktorwet te gebruik?
Hieruit kan ons aflei dat: As die produk van enige twee getalle nul is, dan is een of albei van die getalle nul. Dit wil sê, as ab = 0, dan is a = 0 of b = 0 (wat die moontlikheid insluit dat a = b = 0). Dit word die nulfaktorwet genoem; en ons gebruik dit dikwels om kwadratiese vergelykings op te los
Wat is die vergelyking van kwadratiese funksie?
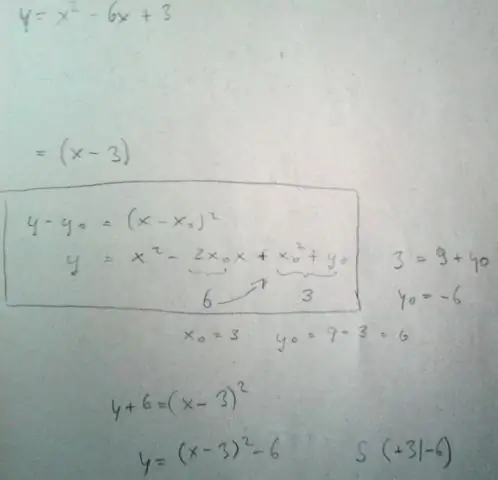
'n Kwadratiese funksie is een van die vorm f(x) = ax2 + bx + c, waar a, b en c getalle is met a nie gelyk aan nul nie. Die grafiek van 'n kwadratiese funksie is 'n kromme wat 'n parabool genoem word. Parabole kan opwaarts of afwaarts oopmaak en wissel in 'breedte' of 'steilheid', maar hulle het almal dieselfde basiese 'U'-vorm
Hoe lyk die grafiek van 'n kwadratiese vergelyking?
Die grafiek van 'n kwadratiese funksie is 'n U-vormige kromme wat 'n parabool genoem word. Dit kan geteken word deur oplossings vir die vergelyking te teken, deur die hoekpunt te vind en die simmetrie-as te gebruik om geselekteerde punte te stip, of deur die wortels en hoekpunt te vind. Die standaardvorm van 'n kwadratiese vergelyking is
Hoe skryf jy 'n kwadratiese vergelyking in C++?
Program 2: vind 'n b en c in 'n kwadratiese vergelyking #include #include int main(){float a,b,c; vlot d,wortel1,wortel2; printf('Voer kwadratiese vergelyking in in die formaat ax^2+bx+c: '); scanf('%fx^2%fx%f',&a,&b,&c); d = b * b - 4 * a * c;
Hoe skakel jy 'n kwadratiese vergelyking om van algemene vorm na standaardvorm?
Enige kwadratiese funksie kan in die standaardvorm f(x) = a(x - h) 2 + k geskryf word waar h en k gegee word in terme van koëffisiënte a, b en c. Kom ons begin met die kwadratiese funksie in algemene vorm en voltooi die vierkant om dit in standaardvorm te herskryf