Video: Hoe vind jy 'n in 'n kwadratiese funksie?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Die kwadratiese funksie f(x) = a(x -h)2 + k, a nie gelyk aan nul nie, word gesê dat dit in standaardvorm is. As a positief is, maak die grafiek opwaarts oop, en as a negatief is, maak dit afwaarts oop. Die simmetrielyn is die vertikale lyn x = h, en die hoekpunt is die punt(h, k).
Daarvan, WAT IS A in die kwadratiese vergelyking?
In algebra, a kwadratiese vergelyking (van die Latynse kwadratus vir "vierkant") is enige vergelyking met die vorm.waar x 'n onbekende voorstel, en a, b en c bekende getalle verteenwoordig, met a ≠ 0. As a = 0, dan is die vergelyking islineêr, nie kwadraties , aangesien daar geen term is nie.
Verder, hoe vind jy die a van 'n parabool? Parabole het altyd 'n laagste punt (of 'n hoogste punt, indien die parabool is onderstebo). Hierdie punt, waar die parabool rigting verander, word die "hoekpunt" genoem. As die kwadratiese in die vorm geskryf word y = a(x –h)2 + k, dan is die hoekpunt die punt (h, k).
Mense vra ook, wat is die 3 vorme van 'n kwadratiese funksie?
Terwyl die meeste van die maniere om die te skryf kwadraties vergelyking is oorbodig en nutteloos, daar is drie vorme wat eintlik unieke gebruike het. Hierdie drie hoof vorms waaruit ons parabole teken, word standaard genoem vorm , onderskep vorm en hoekpunt vorm.
WAT IS A in hoekpuntvorm?
Die hoekpunt vorm van 'n kwadratiese word gegee deur. y =a(x – h)2 + k, waar (h, k) die hoekpunt . Die "a" in die hoekpunt vorm is dieselfde "a" as. in y =ax2 + bx + c (dit wil sê, albei a's het presies dieselfde waarde). Die teken op "a" sê vir jou of die kwadratiese op of af oopmaak.
Aanbeveel:
Wat is die vergelyking van kwadratiese funksie?
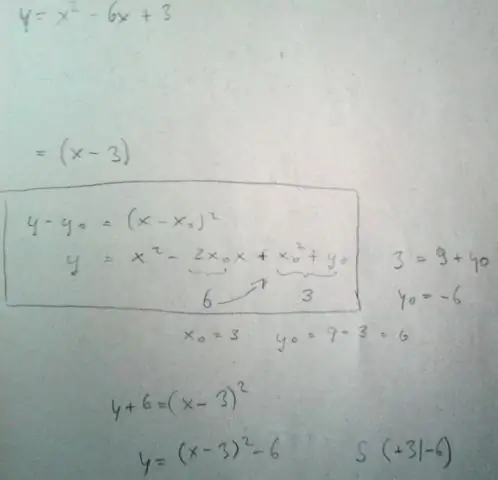
'n Kwadratiese funksie is een van die vorm f(x) = ax2 + bx + c, waar a, b en c getalle is met a nie gelyk aan nul nie. Die grafiek van 'n kwadratiese funksie is 'n kromme wat 'n parabool genoem word. Parabole kan opwaarts of afwaarts oopmaak en wissel in 'breedte' of 'steilheid', maar hulle het almal dieselfde basiese 'U'-vorm
Hoe vind jy die simboliese voorstelling van 'n kwadratiese funksie?
Kwadratiese funksies kan simbolies voorgestel word deur die vergelyking, y(x) = ax2 + bx + c, waar a, b en c konstantes is, en a ≠ 0. Daar word na hierdie vorm verwys as standaardvorm
Hoe vind jy die volgende term in 'n kwadratiese ry?
Skryf die nde term van hierdie kwadratiese getalreeks neer. Stap 1: Bevestig of die ry kwadraties is. Dit word gedoen deur die tweede verskil te vind. Stap 2: As jy die tweede verskil deur 2 deel, sal jy die waarde van a kry
Hoe vind jy die maksimum waarde van 'n kwadratiese funksie?
As jy die formule y = ax2 + bx + c kry, kan jy die maksimum waarde vind deur die formule max =c- (b2 / 4a) te gebruik. As jy die vergelyking y = a(x-h)2 + k het en teaterm is negatief, dan is die maksimum waarde k
Wat is kwadratiese funksie en voorbeelde?
Enkele algemene voorbeelde van die kwadratiese funksie Let op dat die grafiek van die kwadratiese funksie 'n parabool is. Dit beteken dit is 'n kromme met 'n enkele bult. Die grafiek is simmetries oor 'n lyn wat die simmetrie-as genoem word. Die punt waar die simmetrie-as die parabool wat bekend staan as die hoekpunt sny