Hoe vind jy die teenoorgestelde sy van 'n driehoek met Pythagoras?

2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33

Regte Driehoeke en die Pythagoras-stelling

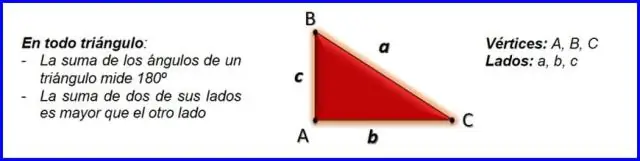
1. Die Pythagoras Stelling, a2+b2=c2, a 2 + b 2 = c 2, kan gebruik word om die lengte van enige kant van 'n reg driehoek .
2. Die kant oorkant die regte hoek word die skuinssy genoem ( kant c in die figuur).

Hierin, hoe vind jy die teenoorgestelde sy van 'n driehoek?

Om uit te vind watter, gee ons eers name aan die kante:

1. Aangrensend is aangrensend (langs) aan die hoek,
2. Oorkant is oorkant die hoek,
3. en die langste sy is die Hipotenuse.

Net so, wat is 'n formule van driehoek? Die Driehoek Formule word hieronder gegee as, Omtrek van a driehoek = a + b + c. Gebied; van; a; driehoek = frac{1}{2}bh. Waar, b die basis van die driehoek . h is die hoogte van die driehoek.

Net so kan 'n mens vra, hoe vind jy die ontbrekende sy van 'n driehoek met een sy en een hoek?

Pythagoras se Stelling (Die Pythagoras Stelling) Die skuinssy is die langste kant van 'n reg driehoek , en is oorkant die regterkant geleë hoek . So, as jy die lengtes van twee ken kante , al wat jy hoef te doen is om die twee lengtes te vier, voeg die resultaat by en neem dan die vierkantswortel van die som om die lengte van die skuinssy te kry.

Hoe vind jy die ontbrekende sy van 'n gelykbenige driehoek?

Om vind 'n onbekende kant van 'n driehoek , jy moet die lengte van ander twee ken kante en/of die hoogte. Om vind die onbekende basis van 'n gelykbenige driehoek , met behulp van die volgende formule : 2 * sqrt(L^2 - A^2), waar L die lengte van die ander twee bene is en A die hoogte van die driehoek.