
- Outeur Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:33.
- Laas verander 2025-06-01 05:03.
VIDEO
Verder, hoe vind jy die inverse van 'n matriks deur 'n identiteitsmatriks te gebruik?
Dit werk op dieselfde manier vir matrikse . As jy a vermenigvuldig matriks (soos A) en sy omgekeerde (in hierdie geval, A-1), kry jy die identiteitsmatriks I. En die punt van die identiteitsmatriks is dat IX = X vir enige matriks X (wat beteken "enige matriks van die regte grootte", natuurlik).
Daarbenewens, wat is die identiteitsmatriks van 'n 3x3? Die identiteitsmatriks of eenheidsmatriks van grootte 3 is die 3x⋅3 3 x ⋅ 3 vierkantige matriks met dié op die hoof diagonaal en nulle elders. In hierdie geval is die identiteitsmatriks ???100010001??? [1 0 0 0 1 0 0 0 1].
Buitendien, hoe vermenigvuldig jy 'n identiteitsmatriks?
Die identiteit eiendom van vermenigvuldiging verklaar dat wanneer 1 is vermenigvuldig met enige reële getal verander die getal nie; dit wil sê, enige getal keer 1 is gelyk aan homself. Die getal "1" word die vermenigvuldiging genoem identiteit vir reële getalle.
Wat gebeur as jy 'n matriks met 'n identiteitsmatriks vermenigvuldig?
Vermenigvuldiging by die identiteit Die " identiteit " matriks is 'n vierkant matriks met 1'e op die diagonaal en nulle oral anders. Vermenigvuldiging van 'n matriks by die identiteitsmatriks I (dit is die hoofletter "oog") verander niks, net soos vermenigvuldig 'n getal by 1 verander niks nie.
Aanbeveel:
Hoe hou die woord matriks verband met mitochondria?
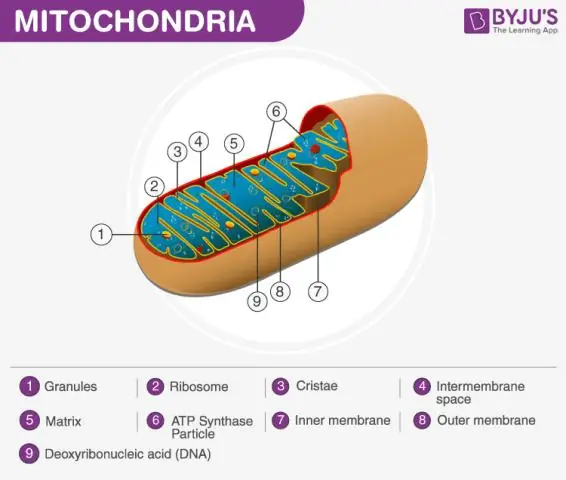
Die mitochondriale matriks Gedefinieer Die mitochondrion bestaan uit 'n buitenste membraan, 'n binnemembraan en 'n jelagtige materiaal wat die matriks genoem word. Hierdie matriks is meer viskeus as die sel se sitoplasma aangesien dit minder water bevat. Dit is 'n belangrike stap in sellulêre respirasie, wat energiemolekules genaamd ATP produseer
Hoe draai jy 'n 45 grade matriks?
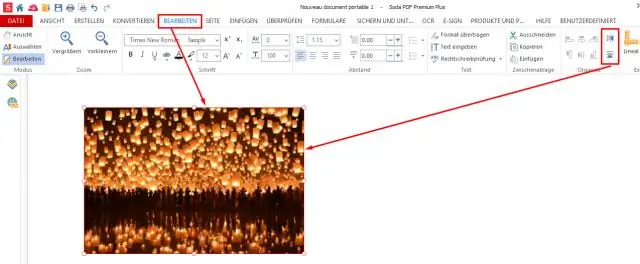
Die formule van hierdie rotasie is: RM[x + y - 1][n - x + y] = M[x][y], waar RM geroteerde matriks beteken, M die aanvanklike matriks, en n die dimensie van die aanvanklike matriks (wat nxn is). Dus, a32, van die derde ry en tweede kolom sal na die vierde ry en die vierde kolom kom
Hoe kan snelheid verander as spoed nie verander nie?

Snelheid is 'n vektorhoeveelheid, wat beteken dit dui grootte en rigting aan. So een manier waarop 'n snelheid van 'n voorwerp kan verander, sonder dat sy spoed verander, is deur sy rigting te verander. 'n Voorbeeld hiervan is in sirkelbeweging, waar 'n voorwerp altyd van rigting verander terwyl dit konstante spoed het
Hoe vind jy die additiewe inverse van 'n matriks?

Om additiewe inverse van gegewe matriks te kry, hoef ons net elke element van matriks met -1 te vermenigvuldig. Wanneer ons elke element van matriks met -1 vermenigvuldig, word dit gelyk aan -A. Gevolglik word A+(-A) gelyk aan 0 waar 0 'n nulmatriks is. Dit voldoen aan die basiese definisie van additiewe inverse
Hoe het mense die eerste keer gewasse verander. Watter metode gebruik wetenskaplikes vandag om gewasse te verander?

Van komkommers en wortels tot wit rys en koring, ons mense het die gene van byna elke kos wat ons eet verander. Vandag kan wetenskaplikes vinnig 'n verandering teweegbring deur 'n enkele geen te kies wat 'n verlangde eienskap tot gevolg kan hê en daardie geen direk in die chromosoom van 'n organisme in te voeg
