INHOUDSOPGAWE:
Video: Is die funksie lineêr of nie-lineêr?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
'n Lineêre funksie is 'n funksie met standaardvorm y = mx + b, waar m die helling is en b die y-afsnit is, en waarvan die grafiek lyk soos 'n reguit lyn. Daar is ander funksies wie se grafiek is nie 'n reguit lyn nie. Hierdie funksies staan bekend as nie-lineêre funksies en hulle kom in baie verskillende vorme voor.
Ook gevra, wat is nie 'n lineêre funksie nie?
Dikwels in ekonomie a lineêre funksie kan nie die verband tussen veranderlikes verduidelik nie. In sulke gevalle 'n nie- lineêre funksie gebruik moet word. Nie- lineêr beteken die grafiek is nie 'n reguit lyn. Die grafiek van 'n nie- lineêre funksie is 'n geboë lyn. 'n Geboë lyn is 'n lyn waarvan die rigting voortdurend verander.
Net so, wat maak 'n funksie lineêr? Lineêre funksies is diegene wie se grafiek 'n reguit lyn is. A lineêre funksie het die volgende vorm. y = f(x) = a + bx. A lineêre funksie het een onafhanklike veranderlike en een afhanklike veranderlike. Die onafhanklike veranderlike is x en die afhanklike veranderlike is y.
Vervolgens kan mens ook vra, watter vergelykings is nie lineêr nie?
Nie-lineêre vergelykings
- 'n Eenvoudige nie-lineêre vergelyking is van die vorm: ax2 + deur2 = c.
- 'n Nie-lineêre vergelyking lyk soos 'n kromme wanneer dit in 'n grafiek geteken word.
- Dit het 'n veranderlike hellingwaarde.
- Die graad van 'n nie-lineêre vergelyking is ten minste 2 of ander hoër heelgetalwaardes.
- Superposisie-beginsel is nie van toepassing op die stelsels wat deur nie-lineêre vergelykings gekenmerk word nie.
Wat is 'n voorbeeld van 'n nie-lineêre funksie?
Algebraïes, lineêr funksies is polinome met die hoogste eksponent gelyk aan 1 of van die vorm y = c waar c konstant is. Nie-lineêre funksies is almal ander funksies . An voorbeeld van 'n nie-lineêre funksie is y = x^2.
Aanbeveel:
Watter verband is nie 'n funksie nie?
Funksies. 'n Funksie is 'n verhouding waarin elke inset slegs een uitset het. In die relasie is y 'n funksie van x, want vir elke invoer x (1, 2, 3 of 0) is daar net een uitset y. x is nie 'n funksie van y nie, want die inset y = 3 het veelvuldige uitsette: x = 1 en x = 2
Hoekom is y vierkantswortel van x nie 'n funksie nie?
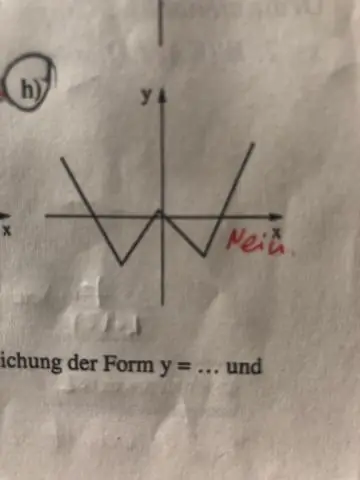
Y=x² kan opgelos word vir x deur die vierkantswortel van beide kante te neem. Die vierkantswortel van 'n getal gee beide 'n positiewe antwoord. x=±√y is nie 'n funksie nie, want vir sommige x-insette (of in hierdie geval byna elke x-invoer), is daar twee verskillende y-uitsette
Hoe weet jy of 'n funksie nie 'n funksie is nie?
Om te bepaal of 'n verband 'n funksie op 'n grafiek is, is relatief maklik deur die vertikale lyntoets te gebruik. As 'n vertikale lyn die verhouding op die grafiek slegs een keer op alle plekke kruis, is die verband 'n funksie. As 'n vertikale lyn egter die relasie meer as een keer kruis, is die relasie nie 'n funksie nie
Wat is die enigste twee letters van die alfabet wat nie op die periodieke tabel voorkom nie?
Die letter 'J' is die enigste letter wat nie in die periodieke tabel voorkom nie
Wat is 'n verband maar nie 'n funksie nie?
'n Funksie is 'n verhouding waarin elke inset slegs een uitset het. In die relasie is y 'n funksie van x, want vir elke invoer x (1, 2, 3 of 0), is daar net een uitset y. x is nie 'n funksie van y nie, want die inset y = 3 het veelvuldige uitsette: x = 1 en x = 2