Video: Het 'n kubieke funksie 'n inverse?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
OOR DIE ALGEMEEN, het GEEN OMGEKEERDE , AS DIT NIE 'N EEN-TOT-EEN IS NIE FUNKSIE ., want net so funksies is omkeerbaar. ? MAAR as a kubieke functionis is van die volgende vorm/kan omgeskakel word na die volgende vorm, dit is omkeerbaar: (i) f(x)=(ax+b)³+c, a≠0, b, c∈|R, met sy natuurlike domein, x∈|R of 'n verminderde domein.
Eenvoudig so, is die inverse van 'n kubieke funksie ook 'n funksie?
Ons sê dat die kubus wortel funksie is die inverse van die kubus funksie . Die vierkant funksie is nie uniek omkeerbaar nie, dus het dit nie 'n omgekeerde funksie . Byvoorbeeld, in enige gegewe jaar is die aantal bagels wat in die VSA verbruik word a funksie van die dag.
Ook, wat is die inverse van 'n polinoom? Die omgekeerde van 'n funksie is die uitdrukking wat jy kry wanneer jy vir x oplos (om die y in die oplossing in x te verander, en die geïsoleerde x in f(x), of y). As gevolg hiervan, vir elke punt [x, y] in die oorspronklike funksie, sal die punt [y, x] op die omgekeerde.
Net so, watter soort funksie is die inverse van 'n kubieke funksie?
Die vind van die kubuswortel en kubering is omgekeerde bewerkings. 'n Funksie kan ook 'n inverse hê. Die inverse funksie van f(x) word geskryf as f-1 (x).
Wat is inverse van 'n funksie?
In wiskunde, 'n omgekeerde funksie (of anti- funksie ) is 'n funksie wat 'n ander "omkeer". funksie : as die funksie f toegepas op 'n inset x gee 'n resultaat van y, en pas dan sy toe omgekeerde funksie g tot y gee die resultaat x, en omgekeerd, dit wil sê, f(x) = y as en slegs as g(y) = x.
Aanbeveel:
Wat is die inverse van 'n eksponensiële funksie?
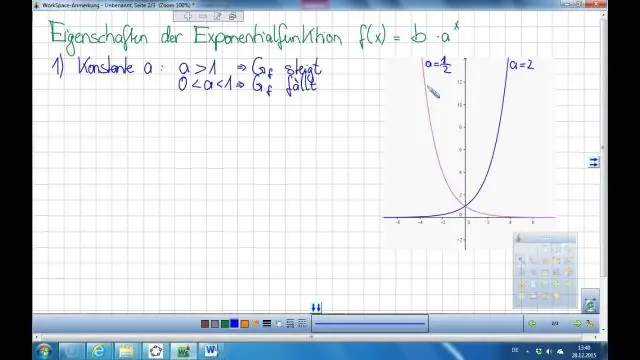
Die inverse van die eksponensiële funksie y = ax is x = ay. Die logaritmiese funksie y = logax word gedefinieer as ekwivalent aan die eksponensiële vergelyking x = ay
Wat is inverse funksie in calculus?
In wiskunde is 'n inverse funksie (of anti-funksie) 'n funksie wat 'n ander funksie 'omkeer': as die funksie f toegepas op 'n inset x 'n resultaat van y gee, dan gee die toepassing van sy inverse funksie g op y die resultaat x, en omgekeerd, dit wil sê, f(x) = y as en slegs as g(y) = x
Wat is die inverse van 'n funksie?
Die inverse van 'n funksie is 'n funksie wat die 'effek' van die oorspronklike funksie omkeer. Gegee 'n funksie, sê f(x), om die inverse van die funksie te vind, verander ons eers f(x) na y. Vervolgens verander ons alle x na y en y na x. en dan los ons op vir y. Die verkrygde oplossing vir y is die inverse van die oorspronklike funksie
Watter vorm maak 'n kubieke funksie?
Vergelykings van hierdie vorm en is in die vorm van 'n parabool, en aangesien b positief is, gaan dit opwaarts aan elke kant van die hoekpunt. Speel met verskeie waardes van b. Soos b groter word, word die parabool steiler en 'smaler'. Wanneer b negatief is, skuins dit afwaarts aan elke kant van die hoekpunt
Wat is 'n kubieke funksie in wiskunde?
Kubieke funksies Die antwoord lê in wat 'n kubieke funksie in wiskunde genoem word. 'n Kubieke funksie kan op 'n paar verskillende maniere beskryf word. Tegnies is 'n kubieke funksie enige funksie van die vorm y = ax^3 + bx^2 + cx + d, waar a, b, c en d konstantes is en a nie gelyk aan nul is nie