INHOUDSOPGAWE:
Video: Wat is inverse funksie in calculus?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
In wiskunde, 'n omgekeerde funksie (of anti- funksie ) is 'n funksie wat 'n ander "omkeer". funksie : as die funksie f toegepas op 'n inset x gee 'n resultaat van y, en pas dan sy toe omgekeerde funksie g tot y gee die resultaat x, en omgekeerd, dit wil sê, f(x) = y as en slegs as g(y) = x.
Gevolglik, hoe vind jy die inverse van 'n funksie in calculus?
Vind die inverse van 'n funksie
- Vervang eers f(x) met y.
- Vervang elke x met 'n y en vervang elke y met 'n x.
- Los die vergelyking van Stap 2 vir y op.
- Vervang y met f−1(x) f − 1 (x).
- Verifieer jou werk deur te kontroleer dat (f∘f−1)(x)=x (f ∘ f − 1) (x) = x en (f−1∘f)(x)=x (f − 1 ∘ f) (x) = x is albei waar.
wat is inverse funksie voorbeeld? Inverse funksies , in die mees algemene sin, is funksies wat mekaar "omkeer". Vir voorbeeld , as f a tot b neem, dan is die omgekeerde , f − 1 f^{-1} f−1f, begin boskrif, minus, 1, eind boskrif, moet b na a neem.
Hierin, hoe onderskei jy inverse funksies?
Afgeleides van inverse trigonometriese funksies
- Gebruik die inverse funksiestelling om die afgeleide van g(x)=sin−1x te vind.
- Aangesien vir x in die interval [−π2, π2], f(x)=sinx die inverse van g(x)=sin−1x is, begin deur f′(x) te vind.
- f′(x)=cosx.
- f′(g(x))=cos(sin−1x)=√1−x2.
- g′(x)=ddx(sin−1x)=1f′(g(x))=1√1−x2.
Wat is 'n self-inverse funksie?
A self inverse funksie is 'n funksie f, sodanig dat y=f(x), met die spesiale eienskap dat ff(x)=x, of anders geskryf, f(x)=f−1(x)
Aanbeveel:
Het 'n kubieke funksie 'n inverse?
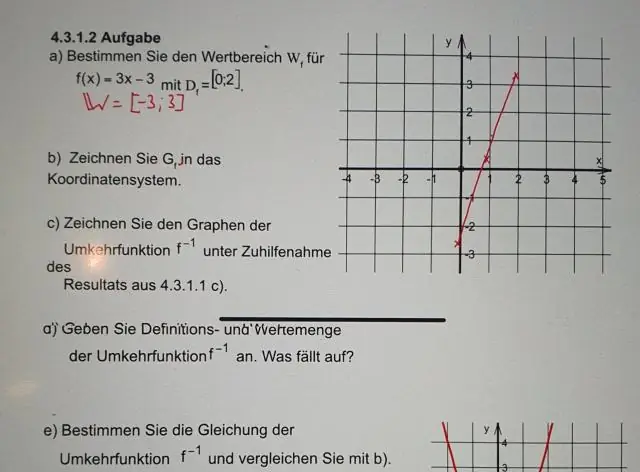
IN DIE ALGEMEEN, het GEEN OMKEER NIE, AS DIT NIE 'N EEN-TOT-EEN FUNKSIE IS NIE., want slegs sulke funksies is omkeerbaar. ? MAAR as 'n kubieke funksionis van die volgende vorm is/kan omgeskakel word na die volgende vorm, is dit omkeerbaar: (i) f(x)=(ax+b)³+c, a≠0, b,c∈|R , met sy natuurlike domein, x∈|R of 'n verminderde domein
Wat is die inverse van 'n eksponensiële funksie?
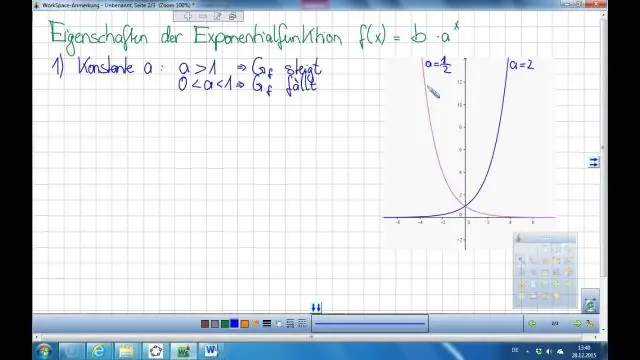
Die inverse van die eksponensiële funksie y = ax is x = ay. Die logaritmiese funksie y = logax word gedefinieer as ekwivalent aan die eksponensiële vergelyking x = ay
Wat is kontinue funksie in calculus?
As 'n funksie kontinu is by elke waarde in 'n interval, dan sê ons dat die funksie kontinu is in daardie interval. En as 'n funksie kontinu is in enige interval, dan noem ons dit eenvoudig 'n kontinue funksie. Calculus gaan in wese oor funksies wat kontinu is op elke waarde in hul domeine
Wat is die inverse van 'n funksie?
Die inverse van 'n funksie is 'n funksie wat die 'effek' van die oorspronklike funksie omkeer. Gegee 'n funksie, sê f(x), om die inverse van die funksie te vind, verander ons eers f(x) na y. Vervolgens verander ons alle x na y en y na x. en dan los ons op vir y. Die verkrygde oplossing vir y is die inverse van die oorspronklike funksie
Wat is 'n saamgestelde funksie in calculus?
Om twee (of meer) funksies soos hierdie te kombineer, word die samestelling van die funksies genoem, en die resulterende funksie word 'n saamgestelde funksie genoem. Die saamgestelde funksiereël wys ons 'n vinniger manier. Reël 7 (Die saamgestelde funksiereël (ook bekend as die kettingreël)) As f(x) = h(g(x)) dan f (x) = h (g(x)) × g (x)