INHOUDSOPGAWE:
Video: Hoe werk funksies in wiskunde?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
In wiskunde , a funksie is 'n verband tussen versamelings wat met elke element van 'n eerste versameling presies een element van die tweede versameling assosieer. Tipiese voorbeelde is funksies van heelgetalle na heelgetalle of van die reële getalle na reële getalle. Byvoorbeeld, die posisie van 'n planeet is a funksie van tyd.
Dan, hoe werk funksies?
A funksie is 'n vergelyking wat net een antwoord vir y vir elke x het. A funksie ken presies een uitset toe aan elke inset van 'n gespesifiseerde tipe. Dit is algemeen om a te noem funksie óf f(x) óf g(x) in plaas van y. f(2) beteken dat ons die waarde van ons moet vind funksie wanneer x gelyk is aan 2.
Weet ook hoekom gebruik ons funksies in wiskunde? Omdat ons maak voortdurend teorieë oor afhanklikhede tussen hoeveelhede in die natuur en die samelewing, funksies is belangrike hulpmiddels in die konstruksie van wiskundig modelle. In skool wiskunde , funksies het gewoonlik numeriese invoere en uitsette en word dikwels deur 'n algebraïese uitdrukking gedefinieer.
Net so, hoe doen jy funksies in wiskunde?
Funksies
- 'n Funksie kan beskou word as 'n reël wat elke lid x van 'n versameling neem en dit toeken, of dit na dieselfde waarde y wat by sy beeld bekend is, afbeeld.
- x → Funksie → y.
- 'n Letter soos f, g of h word dikwels gebruik om vir 'n funksie te staan.
- Voorbeeld.
- f(4) = 42 + 5 =21, f(-10) = (-10)2 +5 = 105 of alternatiewelik f: x → x2 + 5.
Wat is die 4 tipes funksies?
Daar kan 4 verskillende tipes gebruikergedefinieerde funksies wees, dit is:
- Funksie met geen argumente en geen terugkeerwaarde.
- Funksie met geen argumente en 'n terugkeerwaarde.
- Funksie met argumente en geen terugkeerwaarde nie.
- Funksie met argumente en 'n terugkeerwaarde.
Aanbeveel:
Hoe evalueer jy saamgestelde funksies?
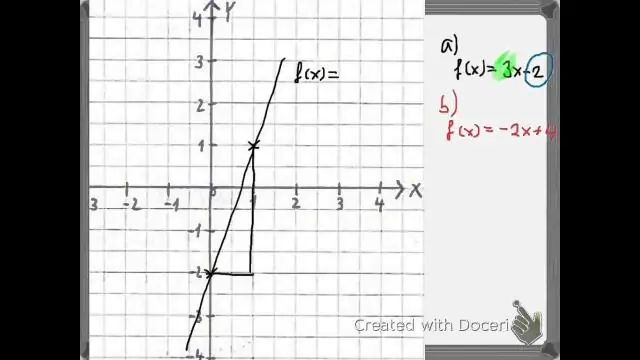
Evaluering van saamgestelde funksies met behulp van grafieke Vind die gegewe invoer na die binneste funksie op die x-as van sy grafiek. Lees die uitset van die binneste funksie vanaf die y-as van sy grafiek af. Vind die binne-funksie-uitset op die x-as van die grafiek van die buitenste funksie
Hoe vermenigvuldig jy saamgestelde funksies?
Vermenigvuldiging en samestelling van funksies Om 'n funksie met 'n skalaar te vermenigvuldig, vermenigvuldig elke uitset met daardie skalaar. Wanneer ons f (g(x)) neem, neem ons g(x) as die invoer van die funksie f. Byvoorbeeld, as f (x) = 10x en g(x) = x + 1, dan vind ons f (g(4)), g(4) = 4 + 1 + 5, en evalueer dan f (5) ) = 10(5) = 50. Voorbeeld: f (x) = 2x - 2, g(x) = x2 - 8
Hoe werk kwadrante in wiskunde?
Die asse van 'n tweedimensionele Cartesiese stelsel verdeel die vlak in vier oneindige streke, genoem kwadrante, elk begrens deur twee halwe asse. Wanneer die asse volgens die wiskundige gebruik geteken word, gaan die nommering antikloksgewys vanaf die regter boonste ('noordoos') kwadrant
Waarom word trigonometriese funksies sirkelvormige funksies genoem?
Trigonometriese funksies word soms sirkelvormige funksies genoem. Dit is omdat die twee fundamentele trigonometriese funksies – die sinus en die cosinus – gedefinieer word as die koördinate van 'n punt P wat rondbeweeg op die eenheidsirkel van radius 1. Die sinus en die cosinus herhaal hul uitsette met gereelde intervalle
Hoe werk radikale in wiskunde?
In wiskunde word 'n radikale uitdrukking gedefinieer as enige uitdrukking wat 'n radikale (√)-simbool bevat. Baie mense noem dit verkeerdelik 'n 'vierkantswortel'-simbool, en baie keer word dit gebruik om die vierkantswortel van 'n getal te bepaal. Byvoorbeeld, 3√(8) beteken om die derdemagswortel van8 te vind