Video: Hoe vind jy die domein van 'n beperking in 'n vergelyking?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Hoe om: Gegee 'n funksie geskryf in 'n vergelyking vorm wat 'n breuk insluit, vind die domein . Identifiseer die invoerwaardes. Identifiseer enige beperkings op die inset. As daar 'n noemer in die funksie se formule , stel die noemer gelyk aan nul en los op vir x.
Net so, hoe vind jy die domein van 'n vergelyking?
Vir hierdie tipe funksie, die domein is alles reële getalle. 'n Funksie met 'n breuk met 'n veranderlike in die noemer. Om vind die domein van hierdie tipe funksie, stel die onderkant gelyk aan nul en sluit die x-waarde jou uit vind wanneer jy die oplos vergelyking . 'n Funksie met 'n veranderlike binne 'n radikale teken.
hoe weet jy of 'n domein alles reële getalle is? Domein is alles reële getalle behalwe 0. Aangesien deling deur 0 ongedefinieerd is, kan (x-3) nie 0 wees nie, en x kan nie 3 wees nie. Domein is alles reële getalle behalwe 3. Aangesien die vierkantswortel van enige nommer minder as 0 is ongedefinieerd, (x+5) moet gelyk aan of groter as nul wees.
Net so, vra mense, wat beteken dit om die domein te beperk?
Beperk domein . Die gebruik van 'n domein vir 'n funksie wat kleiner is as die funksie s'n domein van definisie . Let wel: Beperk domeine word algemeen gebruik om 'n een-tot-een afdeling van 'n funksie te spesifiseer. Sien ook.
Hoe vind jy die beperkings op 'n grafiek?
Om die domein of reeks te beperk (x of y waardes van a grafiek ), kan jy die byvoeg beperking aan die einde van jou vergelyking tussen krullerige hakies {}. Byvoorbeeld, y=2x{1<x<3} sou grafiek die lyn y=2x vir x waardes tussen 1 en 3. Jy kan ook gebruik beperkings op die omvang van 'n funksie en enige gedefinieerde parameter.
Aanbeveel:
Hoe vind jy die vergelyking van die raaklyn van 'n afgeleide?
1) Vind die eerste afgeleide van f(x). 2) Prop xwaarde van die aangeduide punt in f '(x) om die helling by x te vind. 3) Prop x-waarde in f(x) om die y-koördinaat van die tangenspunt te vind. 4) Kombineer die helling van stap 2 en punt van stap 3 deur die punt-helling formule te gebruik om die vergelyking vir die raaklyn te vind
Hoe vind jy die asimptoot van 'n logaritmiese vergelyking?
Sleutelpunte Wanneer 'n grafiek geteken word, is die logaritmiese funksie soortgelyk in vorm aan die vierkantswortelfunksie, maar met 'n vertikale asimptoot soos x 0 van regs nader. Die punt (1,0) is op die grafiek van alle logaritmiese funksies van die vorm y=logbx y = l o g b x, waar b 'n positiewe reële getal is
Watter van die volgende verteenwoordig die molekulêre vergelyking vir die reaksie van waterige ammoniak met swaelsuur die beste?
Vraag: Die gebalanseerde vergelyking vir die reaksie van waterige swaelsuur met waterige ammoniak is 2NH3(aq) + H2SO4 (aq) --> (NH4)2SO4(aq) A
Hoe vind jy die vergelyking van die middellyn van 'n lynstuk?
Skryf 'n vergelyking in punt-helling vorm, y - k =m(x - h), aangesien die helling van die loodregte middellyn en 'n punt (h, k) waardeur die middellyn gaan bekend is. Los die punt-helling-vergelyking vir y op om y = mx + b te kry. Versprei die hellingwaarde. Skuif die k-waarde na die regterkant van die vergelyking
Hoe vind jy die domein van 'n algebraïese funksie?
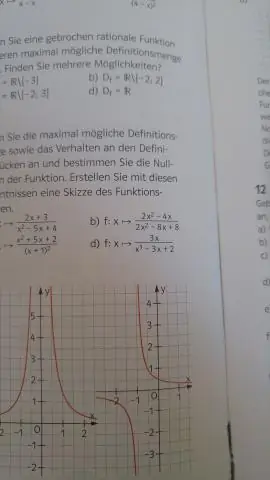
Die domein van 'n funksie is die stel van alle moontlike insette vir die funksie. Byvoorbeeld, die domein van f(x)=x² is alle reële getalle, en die domein van g(x)=1/x is alle reële getalle behalwe vir x=0