Video: Hoe vind jy die domein van 'n algebraïese funksie?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Die domein van 'n funksie is die stel van alle moontlike insette vir die funksie . Byvoorbeeld, die domein van f(x)=x² is alle reële getalle, en die domein van g(x)=1/x is alle reële getalle behalwe x=0.
Hiervan, hoe vind jy die domein van 'n funksie?
Vir hierdie tipe van funksie , die domein is alles reële getalle. A funksie met 'n breuk met 'n veranderlike in die noemer. Om die domein van hierdie tipe funksie , stel die onderkant gelyk aan nul en sluit die x-waarde uit wat jy kry wanneer jy die vergelyking oplos. A funksie met 'n veranderlike binne 'n radikale teken.
Tweedens, hoe vind jy 'n funksie op 'n grafiek? Die vertikale lyntoets kan gebruik word om te bepaal of a grafiek verteenwoordig a funksie . 'n Vertikale lyn sluit alle punte met 'n bepaalde x-waarde in. Die y-waarde van 'n punt waar 'n vertikale lyn a sny grafiek verteenwoordig 'n uitset vir daardie invoer x waarde.
Verder, hoe vind jy die domein en omvang van 'n funksie?
Nog 'n manier om die domein en reeks van funksies is deur grafieke te gebruik. Omdat die domein verwys na die stel moontlike insetwaardes, die domein van 'n grafiek bestaan uit al die invoerwaardes wat op die x-as getoon word. Die reeks is die stel moontlike uitsetwaardes wat op die y-as getoon word.
Wat is die domein in algebra?
Die domein van 'n funksie is die volledige stel moontlike waardes van die onafhanklike veranderlike. In gewone Engels beteken hierdie definisie: Die domein is die stel van alle moontlike x-waardes wat die funksie sal laat "werk", en werklike y-waardes sal uitvoer.
Aanbeveel:
Wat is die praktiese domein en omvang van jou funksie?
Die moontlike waardes van 'y' word die reeks genoem. Teoretiese domeine en reekse handel oor alle moontlike oplossings. Praktiese domeine en reekse vernou die oplossingsstelle om realisties te wees binne gedefinieerde parameters
Hoe vind jy die tweede afgeleide van 'n trig-funksie?
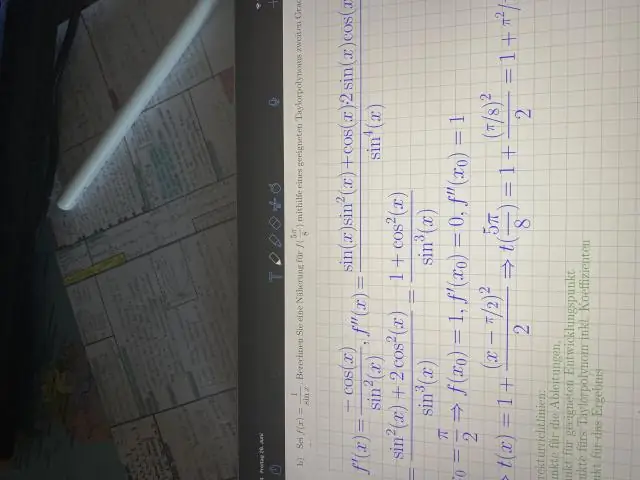
VIDEO Net so, wat is die afgeleides van die 6 trig-funksies? Afgeleides van trigonometriese funksies. Die basiese trigonometriese funksies sluit die volgende 6 funksies in: sinus ( sonde x), kosinus ( cos x), tangens (tanx), cotangens (cotx), secant (secx) en cosecant (cscx).
Hoe vind jy die simboliese voorstelling van 'n kwadratiese funksie?
Kwadratiese funksies kan simbolies voorgestel word deur die vergelyking, y(x) = ax2 + bx + c, waar a, b en c konstantes is, en a ≠ 0. Daar word na hierdie vorm verwys as standaardvorm
Hoe vind jy die funksie van 'n sirkel?
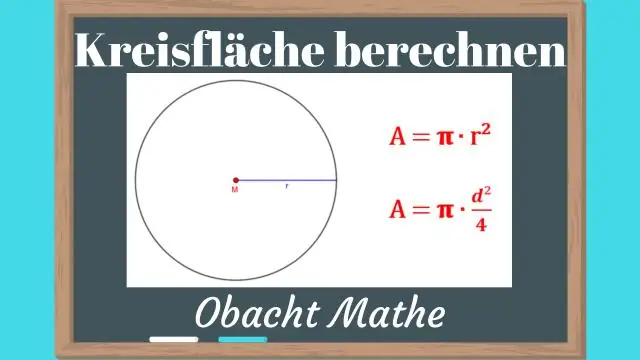
Die middel-radius-vorm van die sirkelvergelyking is in die formaat (x – h)2 + (y – k)2= r2, met die middelpunt by die punt (h, k) en die radius is 'r'. Hierdie vorm van die vergelyking is nuttig, aangesien jy maklik die middelpunt en die radius kan vind
Hoe vind jy die domein van 'n beperking in 'n vergelyking?
Hoe om: Gegee 'n funksie geskryf in 'n vergelykingsvorm wat 'n breuk insluit, vind die domein. Identifiseer die invoerwaardes. Identifiseer enige beperkings op die insette. As daar 'n noemer in die funksie se formule is, stel die noemer gelyk aan nul en los vir x op