INHOUDSOPGAWE:
Video: Hoe los jy absolute funksies op?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
OPLOSSING VAN VERGELYKINGS WAT ABSOLUTE WAARDE BEVAT
- Stap 1: Isoleer die absoluut waarde uitdrukking.
- Stap 2: Stel die hoeveelheid binne die absoluut waardenotasie gelyk aan + en - die hoeveelheid aan die ander kant van die vergelyking.
- Stap 3: Los op vir die onbekende in beide vergelykings .
- Stap 4: Gaan jou antwoord analities of grafies na.
Op hierdie manier, hoe vind jy die absolute waarde?
Die absolute waarde van 'n getal is die getal se afstand vanaf nul, wat altyd positief sal wees waarde . Om vind die absolute waarde van 'n getal, laat val die negatiewe teken as daar een is om die getal positief te maak. Byvoorbeeld, negatiewe 4 sal 4 word.
Die vraag is dan, wat is die simbool vir absolute waarde? Die simbool vir absolute waarde is twee reguit lyne wat die getal of uitdrukking omring waarvoor jy wil aandui absolute waarde . |6| = 6 beteken die absolute waarde van 6 is 6.
Om ook te weet, wat is die reëls vir absolute waarde?
Wanneer ons die absolute waarde van 'n getal, eindig ons altyd met 'n positiewe getal (of nul). Of die inset positief of negatief (of nul) was, die uitset is altyd positief (of nul). Byvoorbeeld, | 3 | = 3, en | –3 | = 3 ook.
Hoe los jy stelsel van vergelykings op?
Volg die stappe om die probleem op te los
- Stap 1: Vermenigvuldig die hele eerste vergelyking met 2.
- Stap 2: Herskryf die stelsel van vergelykings, en vervang die eerste vergelyking met die nuwe vergelyking.
- Stap 3: Voeg die vergelykings by.
- Stap 4: Los op vir x.
- Stap 5: Vind die y-waarde deur x in enige vergelyking in 3 te vervang.
Aanbeveel:
Hoe werk funksies in wiskunde?
In wiskunde is 'n funksie 'n verband tussen versamelings wat met elke element van 'n eerste versameling presies een element van die tweede versameling assosieer. Tipiese voorbeelde is funksies van heelgetalle tot heelgetalle of van die reële getalle na reële getalle. Byvoorbeeld, die posisie van 'n planeet is 'n funksie van tyd
Hoe evalueer jy saamgestelde funksies?
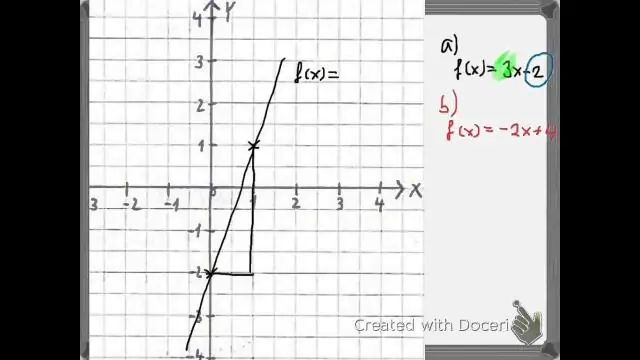
Evaluering van saamgestelde funksies met behulp van grafieke Vind die gegewe invoer na die binneste funksie op die x-as van sy grafiek. Lees die uitset van die binneste funksie vanaf die y-as van sy grafiek af. Vind die binne-funksie-uitset op die x-as van die grafiek van die buitenste funksie
Hoe vermenigvuldig jy saamgestelde funksies?
Vermenigvuldiging en samestelling van funksies Om 'n funksie met 'n skalaar te vermenigvuldig, vermenigvuldig elke uitset met daardie skalaar. Wanneer ons f (g(x)) neem, neem ons g(x) as die invoer van die funksie f. Byvoorbeeld, as f (x) = 10x en g(x) = x + 1, dan vind ons f (g(4)), g(4) = 4 + 1 + 5, en evalueer dan f (5) ) = 10(5) = 50. Voorbeeld: f (x) = 2x - 2, g(x) = x2 - 8
Hoe los jy 'n absolute waardevergelyking algebraïes op?
OPLOSSING VAN VERGELYKINGS WAT ABSOLUTE WAARDE(S) BEVAT Stap 1: Isoleer die absolute waarde-uitdrukking. Stap2: Stel die hoeveelheid binne die absolute waarde notasie gelyk aan + en - die hoeveelheid aan die ander kant van die vergelyking. Stap 3: Los op vir die onbekende in beide vergelykings. Stap 4: Gaan jou antwoord analities of grafies na
Waarom word trigonometriese funksies sirkelvormige funksies genoem?
Trigonometriese funksies word soms sirkelvormige funksies genoem. Dit is omdat die twee fundamentele trigonometriese funksies – die sinus en die cosinus – gedefinieer word as die koördinate van 'n punt P wat rondbeweeg op die eenheidsirkel van radius 1. Die sinus en die cosinus herhaal hul uitsette met gereelde intervalle