Video: Wat is die inverse hiperboliese sinusfunksie?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Die hiperboliese sinusfunksie , sinhx, is een-tot-een, en het dus 'n goed gedefinieerde omgekeerde , sinh−1x, getoon in blou in die figuur. Volgens konvensie word cosh−1x geneem om die positiewe getal y te beteken sodat x = koshy.
Wat is dan die omgekeerde van cosh?
Die funksie kos is ewe, so formeel gesproke het dit nie 'n omgekeerde , om basies dieselfde rede dat die funksie g(t)=t2 nie an het nie omgekeerde . Maar as ons beperk die domein van kos gepas, dan is daar 'n omgekeerde . Die gewone definisie van kos −1x is dat dit die nie-negatiewe getal is wie se kos is x.
Behalwe hierbo, wat is Arcos? arccosh (x) verteenwoordig die inverse van die hiperboliese cosinusfunksie. arccosh word gedefinieer vir komplekse argumente. Wisselpuntwaardes word teruggestuur vir drywendepuntargumente. Swewende-punt-intervalle word teruggestuur vir drywende-punt-interval argumente. Ongeëvalueerde funksie-oproepe word vir die mees presiese argumente teruggestuur.
Buitendien, is Sinh dieselfde as inverse sinus?
Geen, sinh is 'n hiperboliese funksie van sinus . Sonde ^-1 is omgekeerde van sinus . Jy gebruik die omgekeerde om hoeke te vind.
Wat is die omgekeerde van Sinh?
Die hiperboliese sinus funksie, sinh x, is een-tot-een, en het dus 'n goed gedefinieerde omgekeerde , sinh −1x, getoon in blou in die figuur. Om die om te keer hiperboliese cosinus-funksie moet ons egter (soos met vierkantswortel) sy domein beperk.
Aanbeveel:
Hoe teken jy 'n hiperboliese funksie?
Grafieke van hiperboliese funksies sinh(x) = (e x - e -x)/2. cosh(x) = (e x + e -x)/2. tanh(x) = sinh(x) / cosh(x) = (ex - e -x) / (ex + e -x) coth(x) = cosh(x) / sinh(x) = (ex + e - x) / (ex - e -x) sech(x) = 1 / cosh(x) = 2 / (ex + e -x) csch(x) = 1 / sinh(x) = 2 / (ex - e - x)
Wat is die verskil tussen inverse en ontkenning?
As 'n stelling se omgekeerde waar is, dan is die omgekeerde daarvan waar (en omgekeerd). As 'n stelling se omgekeerde vals is, dan is die omgekeerde daarvan vals (en omgekeerd). As 'n stelling se ontkenning onwaar is, dan is die stelling waar (en omgekeerd)
Wat is die inverse van 'n eksponensiële funksie?
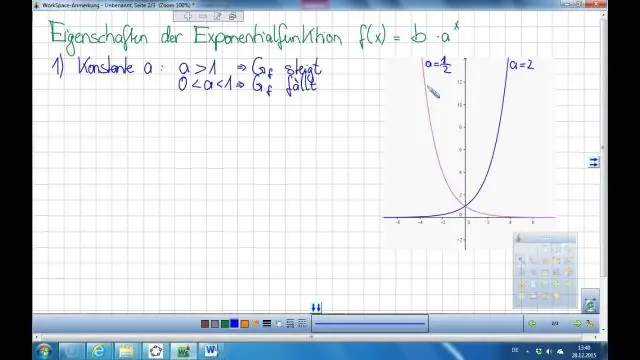
Die inverse van die eksponensiële funksie y = ax is x = ay. Die logaritmiese funksie y = logax word gedefinieer as ekwivalent aan die eksponensiële vergelyking x = ay
Wat is die domein en omvang van die sinusfunksie?
Die sinus- en cosinusfunksies het 'n periode van 2π radiale en die raaklynfunksie het 'n periode van π radiale. Domein en reeks: Uit die grafiek hierbo sien ons dat vir beide die sinus- en cosinusfunksies die domein alle reële getalle is en die reeks is alle reëls van −1 tot +1inklusief
Sny parallelle lyne in hiperboliese meetkunde?
In hiperboliese meetkunde is daar twee soorte parallelle lyne. As twee lyne nie in 'n model van hiperboliese meetkunde sny nie, maar hulle sny wel op die grens daarvan, word die lyne asimptoties parallel of hiperparallel genoem