Video: Hoe vind jy die hoekpunt van 'n horisontale parabool?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
As 'n parabool het 'n horisontaal as, die standaardvorm van die vergelyking van die parabool is dit: (y -k)2 = 4p(x - h), waar p≠ 0. Die hoekpunt van hierdie parabool is by (h, k). Die fokus is by (h + p, k). Die rigting is die lyn x = h - p.
Net so, hoe vind jy die hoekpunt en rigting van 'n parabool?
Die standaardvorm is (x - h)2 = 4p (y - k), waar die fokus is (h, k + p) en die riglyn is y= k - p. As die parabool word gedraai sodat sy hoekpunt is (h, k) en sy simmetrie-as is parallel aan die x-as, dit het 'n vergelyking van (y - k)2 = 4p (x -h), waar die fokus is (h + p, k) en die riglyn is x = h - p.
Daarbenewens, wat is die vergelyking vir 'n sywaartse parabool? Die "algemene" vorm van 'n parabool se vergelyking is die een waaraan jy gewoond is, y = byl2 + bx + c - tensy die kwadratiese is " sywaarts ", in welke geval die vergelyking sal iets soos x = ay lyk2 + deur +c.
Net so, hoe vind jy die hoekpunt van 'n paraboolvergelyking?
Hierdie punt, waar die parabool verander rigting, word die " hoekpunt ". As die kwadratiese in die vorm geskryf word y = a(x – h)2 + k, dan die hoekpunt is die punt (h, k). Dit maak sin, as jy daaroor dink. Die vierkantige deel is altyd positief (vir 'n regterkant na bo parabool ), tensy dit nul is.
Vir watter waarde van p het die hoekpunt van die parabool?
Die absolute waarde van p is die afstand tussen die hoekpunt en die fokus en die afstand tussen die hoekpunt en die riglyn. (Die teken aan bl vertel my op watter manier die parabool gesigte.) Aangesien die fokus en rigting twee eenhede uitmekaar is, moet hierdie afstand een eenheid wees, dus | bl | = 1.
Aanbeveel:
Hoe vind jy die horisontale strek?
Indien b>1, strek die grafiek met betrekking tot die y -as, of vertikaal. Indien b<1, krimp die grafiek ten opsigte van die y -as. Oor die algemeen word 'n horisontale strek gegee deur die vergelyking y=f(cx) y = f (c x)
Hoe vind jy die hoekpunt en Directrice?
Die standaardvorm is (x - h)2 = 4p (y - k), waar die fokus (h, k + p) is en die riglyn y = k - p is. As die parabool so gedraai word dat sy hoekpunt (h,k) is en sy simmetrie-as parallel aan die x-as is, het dit 'n vergelyking van (y - k)2 = 4p (x - h), waar die fokus is (h + p, k) en die riglyn is x = h - p
Hoe benoem jy die hoekpunt en simmetrie-as?
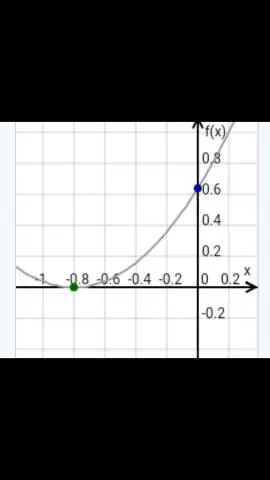
Die simmetrie-as gaan altyd deur die hoekpunt van die parabool. Die x -koördinaat van die hoekpunt is die vergelyking van die simmetrie-as van die parabool. Vir 'n kwadratiese funksie in standaardvorm, y=as2+bx+c, is die simmetrie-as 'n vertikale lyn x=−b2a
Hoe teken jy 'n keël van 'n parabool?
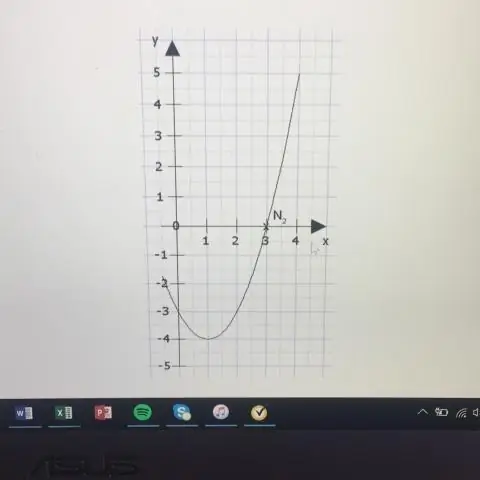
Die riglyn is die lyn y = k - p. Die as is die lyn x = h. As p > 0, maak die parabool opwaarts oop, en as p < 0, maak die parabool afwaarts oop. As 'n parabool 'n horisontale as het, is die standaardvorm van die vergelyking van die parabool die volgende: (y - k)2 = 4p(x - h), waar p≠ 0
Hoe vind jy die horisontale raaklyn?
Horisontale lyne het 'n helling van nul. Daarom, wanneer die afgeleide nul is, is die raaklyn horisontaal. Om horisontale raaklyne te vind, gebruik die afgeleide van die funksie om die nulle op te spoor en prop dit terug in die oorspronklike vergelyking