INHOUDSOPGAWE:
Video: Hoe vind jy die hoekpunt en Directrice?
2024 Outeur: Miles Stephen | [email protected]. Laas verander: 2023-12-15 23:33
Die standaardvorm is (x - h)2 = 4p (y - k), waar die fokus is (h, k + p) en die riglyn is y = k - p. As die parabool so gedraai word dat sy hoekpunt is (h, k) en sy simmetrie-as is parallel aan die x-as, dit het 'n vergelyking van (y - k)2 = 4p (x - h), waar die fokus is (h + p, k) en die riglyn is x = h - p.
Net so, hoe vind jy die hoekpuntvorm van 'n parabool?
f (x) = a(x - h)2 + k, waar (h, k) die hoekpunt van die parabool . FYI: Verskillende handboeke het verskillende interpretasies van die verwysing "standaard vorm " van 'n kwadratiese funksie. Sommige sê f (x) = ax2 + bx + c is "standaard vorm ", terwyl ander sê dat f (x) = a(x - h)2 + k is "standaard vorm ".
Mens kan ook vra, hoe skryf jy 'n vergelyking vir 'n parabool? Vir parabole wat op of af oopmaak, die standaardvorm vergelyking is (x - h)^2 = 4p(y - k). Vir parabole wat sywaarts oopmaak, die standaardvorm vergelyking is (y - k)^2 = 4p(x - h). Die hoekpunt of punt van ons parabool word gegee deur die punt (h, k).
Mens kan ook vra, hoe vind jy die hoekpunt?
Stappe om op te los
- Kry die vergelyking in die vorm y = ax2 + bx + c.
- Bereken -b / 2a. Dit is die x-koördinaat van die hoekpunt.
- Om die y-koördinaat van die hoekpunt te vind, prop eenvoudig die waarde van -b / 2a in die vergelyking vir x en los vir y op. Dit is die y-koördinaat van die hoekpunt.
Wat is P in 'n parabool?
A parabool is die versameling punte in die vlak wat ewe ver van F en d is. Die punt F word die fokus genoem en die lyn d word die riglyn genoem. Die punt P is 'n tipiese punt op die parabool sodat sy afstand vanaf die rigting, PQ, gelyk is aan sy afstand vanaf F, PF.
Aanbeveel:
Hoe skakel jy standaard hoekpunt om na gefaktoriseerde vorm?
Omskakeling tussen verskillende vorme van 'n kwadratiese - Expii. Standaardvorm is ax^2 + bx + c. Topvorm is a(x-h)^2 + k, wat die hoekpunt en simmetrie-as openbaar. Gefaktoriseerde vorm is a(x-r)(x-s), wat die wortels openbaar
Wat is die Directrice in 'n parabool?
Directix. 'n Parabool is 'n versameling van alle punte in 'n vlak wat 'n gelyke afstand van 'n gegewe punt en gegewe lyn af is. Die punt word die fokus van die parabool genoem, en die lyn word die rigting genoem. Die rigting is loodreg op die simmetrie-as van 'n parabool en raak nie aan die parabool nie
Hoe benoem jy die hoekpunt en simmetrie-as?
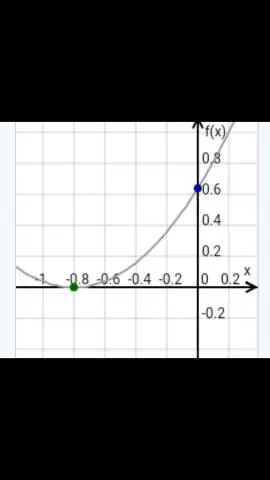
Die simmetrie-as gaan altyd deur die hoekpunt van die parabool. Die x -koördinaat van die hoekpunt is die vergelyking van die simmetrie-as van die parabool. Vir 'n kwadratiese funksie in standaardvorm, y=as2+bx+c, is die simmetrie-as 'n vertikale lyn x=−b2a
Hoe vind jy die hoekpunt van 'n horisontale parabool?
As 'n parabool 'n horisontale as het, is die standaardvorm van die vergelyking van die parabool dit: (y -k)2 = 4p(x - h), waar p≠ 0. Die hoekpunt van hierdie parabool is by (h, k). Die fokus is by (h + p, k). Die rigting is die lyn x = h - p
Hoe vind jy die area van die gesig deur die oppervlakte te gebruik?
Oppervlakte is die som van die oppervlaktes van alle vlakke (of oppervlaktes) op 'n 3D-vorm. 'n Kubus het 6 reghoekige vlakke. Om die oppervlakte van 'n blokkie te vind, voeg die oppervlaktes van al 6 vlakke by. Ons kan ook die lengte (l), breedte (w) en hoogte (h) van die prisma benoem en die formule, SA=2lw+2lh+2hw, gebruik om die oppervlakte te vind